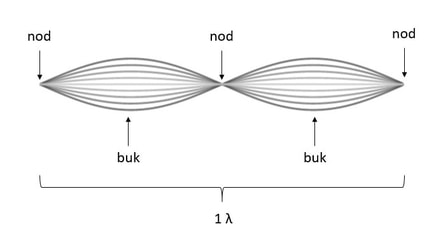
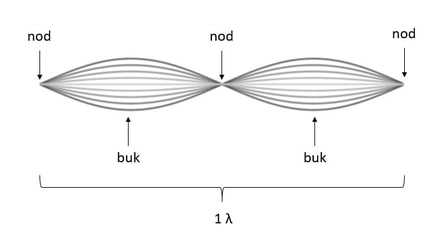
vågor
 Vad är svängningsbukar för något?
Vad är svängningsbukar för något?
a) tror jag är våglängd= v hastighet / f frekvens
men svaret känner jag att de hör till dessa svängningsbukar.
b) frekvensen förändras inte tror jag.
eller att
f=v/våglängd * svängbukar 1/4
Där stående vågor får maximalt utslag.
Använd dessa samband:
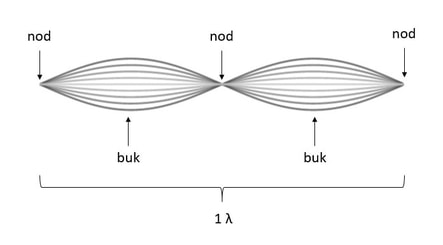
Mrpotatohead skrev:Där stående vågor får maximalt utslag.
Använd dessa samband:
Finns det något matematiskt sätt o beräkna dessa bukningar?
Eller hur ska jag tänka för att komma ihåg dem lätt, det är ju lätt o glömma bort dem ifall man ska bara försöka på sig att komma ihåg en tabell. Då jag hittar inga tabeller i min formelsamling om bukningar.
micke2z skrev:Mrpotatohead skrev:Där stående vågor får maximalt utslag.
Använd dessa samband:
Finns det något matematiskt sätt o beräkna dessa bukningar?
Eller hur ska jag tänka för att komma ihåg dem lätt, det är ju lätt o glömma bort dem ifall man ska bara försöka på sig att komma ihåg en tabell. Då jag hittar inga tabeller i min formelsamling om bukningar.
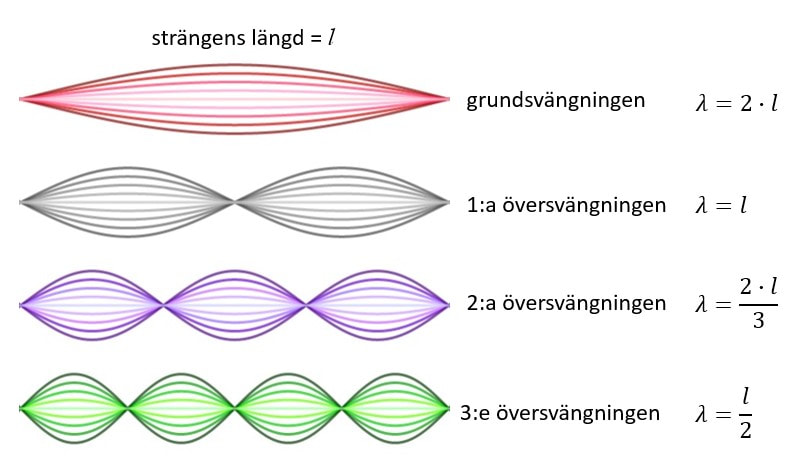
Eller jag tro att jag hittat formlerna. L=n*2/våglängd och L=((2n-1)*våglängd)/4
a) L = n * våglängd /2
våglängd = L*2/3 = 0.8
v=våglängd *frekvens => 0.8*22= 17.6 m/s
b) våglängd = 2*L/n => 2*0.12/4=0.6
f=v/våglängd => våglängd = 0,6 , v=17.6m/s => 17.6/0,6=29.6666... ungefär 30 hz
Bra jobbat!
Om du vill se med egna ögon att (och varför) vissa svängningsfrekvenser kommer att förstärkas kraftigt och skapa stående vågor med noder (”nodes” på engelska) och bukar (”anti-nodes” på engelska) enligt den formel som du hittade, så titta på den här korta simuleringen.