Våglängder
En uppgift jag har börjat på och har fastnat, jag kan ej fortsätta hur mycket jag än tänker. Jag har beräknat våglängden och sedan antalet våglängder som det finns mellan högtalare 1 och punkten A, men sedan efter det har jag det svårt att fortsätta! Uppskattar all hjälp jag får! Här är uppgiften:
Två små högtalare H1 och H2 sänder ut ljudvågor med frekvensen 0,90 kHz. Högtalarnas membraner svänger i fas med varandra. Högtalaren H1 är fast placerad medan H2 kan förflyttas utmed linjen DE. En mikrofon är placerad i punkten A, 1,5 m rakt framför H1. Högtalarna är från början placerade intill varandra. Då H2 förflyttas från H1 mot E minskar först ljudstyrkan i punkten A för att sedan öka till ett maximum då avståndet mellan högtalarna är s. Bestäm avståndet s.
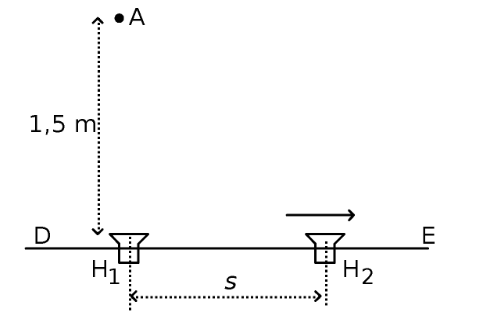
Vad är vägskillnaden (uttryckt i våglängder) i A när du har ditt första maximum i A?
Våglängden hade du räknat ut.
Vägskillnaden kan du även räkna ut rent geometriskt, uttryckt i s.
Är det en lambdas skillnad/en våglängds?
Ja, en våglängds vägskillnad.
Är du med på varför?
Nej, tyvärr inte! :(
Högtalarna är från början placerade intill varandra. Då H2 förflyttas från H1 mot E minskar först ljudstyrkan i punkten A för att sedan öka till ett maximum då avståndet mellan högtalarna är s.
Vägskillnaden är från början liten (högtalarna intill varandra). När H2 flyttas mot E så ökar vägskillnaden och interferensen blir först mindre konstruktiv i A. Första minimum nås i A när vägskillnaden är en halv våglängd. Efter det så blir interferensen mer konstruktiv och första maximum fås när vägskillnaden är en hel våglängd.
Tack så mycket för hjälpen! :)


