Vågfysik Longitudinell vågor

Bestäm först vågens utbredningshastighet.

Lite osäker på hur man kommer vidare med det? frekvensen får vi fram då vi har vinkelfrekvensen sedan antar jag att våglängden är 1.6m eftersom jag tror de menar att 0.8m är en halv våglängd. Lite ösäker på detta. Men iallafall sen kan man få fram hastigheten genom att multiplicera frekvensen och våglängden. Men hur kommer man vidare efter detta?

MagicXXX skrev:

jag tror de menar att 0.8m är en halv våglängd.  

Jag tror att de skriver att våglängden är 8 cm.

Så vid 12 cm svänger punkten i motfas med origo.

Punkten vid 10 cm ligger mitt emellan.

Gör några skissar. 

Det verkar som x=10 är en extrem punkt men hur kan jag använda detta för att komma vidare?

MagicXXX skrev:

Det verkar som x=10 är en extrem punkt men hur kan jag använda detta för att komma vidare?

Vad menar du med extrem punkt?

Punkten vid 10 cm ligger 90^o efter 8 cm (och origo) och 90^o före 12 cm (som är i motfas med origo)

x=10 är ju precis var sinus har sitt max/min värde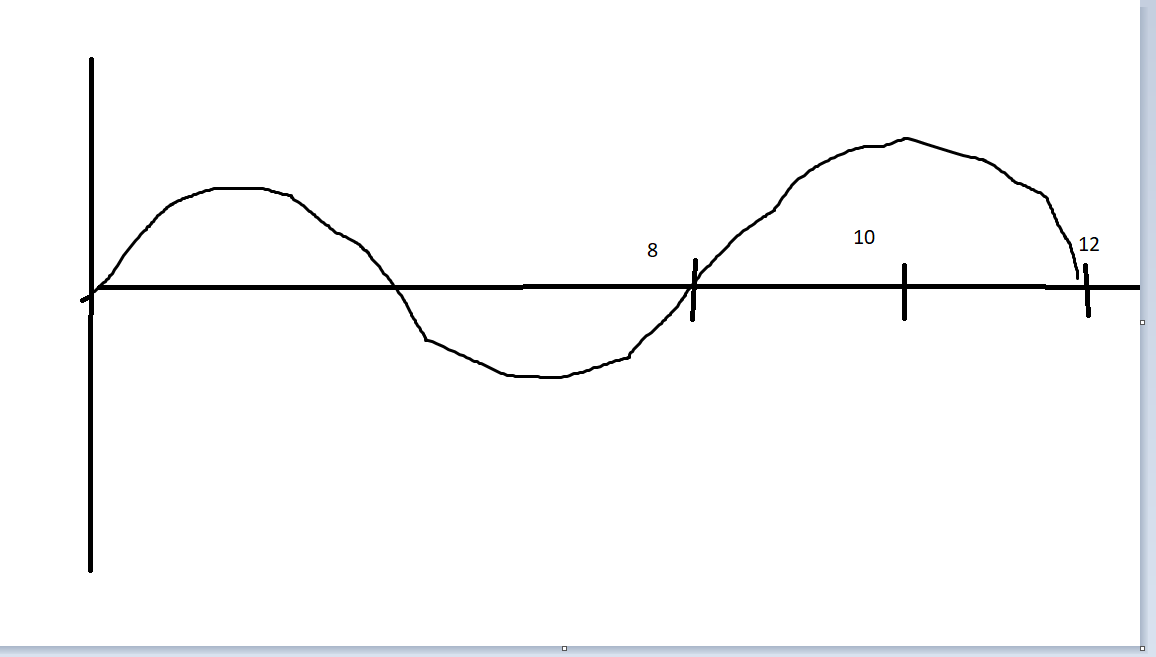

Vid vilken tid skulle detta vara?

(Och det är en mycket grov skiss.)

Det är väl inte det vi letar efter?  Vi försöker väl hitta när x=10 korsar x linjen? alltså y=0.

Tiden kan man väl få fram genom att använda x=v*t eftersom den givna funktionen endast beskriver svängningen vid origo

Jo, därför föreslog jag att man kunde börja med att bestämma utbredningshastighet.

Men om man ska reda ut vad som händer som funktion av tid efter t=0 på ett grafiskt sätt, är det naturligt att börja rita utslaget vid t=0.

Tror jag förstod nu, om man använder x=v*t och löser ut tiden då får man ju tiden det tar för vågen vid origo att ta sig till punkten 10, och det är precis det vi är efter. men jag verkar inte få rätt svar. ω=2pi*f=20pi, detta innebär att f=10Hz. Hastigheten är ju våglängden*frekvensen, alltså 8m/s. x=0.1m  och genom x=v*t bör tiden vara 0.0125s. Men i facit står det att det är 17ms. Vad är det jag tänker fel?

MagicXXX skrev:

f=10Hz. Hastigheten är ju våglängden*frekvensen, alltså 8m/s.  

Jag har redan skrivit: "Jag tror att de skriver att våglängden är 8 cm."

Men du verkar inte hålla med om det.

Oj missade att det var i cm och inte m alltså blir det 0.08*10=0.08m/s, men det ger fortfarande inte rätt svar.

Blir du klokare av denna plot?

Tillägg: 5 feb 2022 00:35

Denna animation kan nog hjälpa avsevärt också:

https://www.geogebra.org/m/YKuG3zNZ

Hastigheten är ju våglängden*frekvensen, alltså 8m/s. x=0.1m  och genom x=v*t bör tiden vara 0.0125s. Men i facit står det att det är 17ms. Vad är det jag tänker fel?

Vågen ska inte röra sig ett avstånd på 10 cm; den ska röra sig så långt att punkten vid x = 10 cm når y = 0. Vill du lösa uppgiften utan att tänka kan du använda vågbeskrivningen:

$y(x,t)=A\sin(kx-\omega t + \phi)$

Lös den trigonometriska ekvationen $y(0.1,t) = 0$ för lägsta möjliga $t>0$ så har du ditt svar.

Tack för det detaljerad svaret, men jag får inte riktigt till ekvationen, ω ska väl vara 20pi? k löser vi ut, och ϕ bör väl vara pi/6?

MagicXXX skrev:

ω ska väl vara 20pi?

Ja.

k löser vi ut

Nej, $k = 2\pi/\lambda$.

och ϕ bör väl vara pi/6?

Ja.

Edit: Jag ville egentligen inte prata om detta men jag måste förklara då du inte verkar vara så bevandrad med vågekvationen. I formen som den är given i uppgiften har vi att skalärprodukten mellan vågvektorn $\vec{k}$ och x-vektorn $\vec{x}$ är negativ. Detta vet vi därför att de beskrivit vågen på formen:

$s(x,t)=A\sin(\omega t - kx +\phi)$

Där vi i origo har att:

$s(0,t) = A\sin(\omega t + \phi)$

Vi vet att vågvektorn är riktad i positivt x-led enligt uppgiften. Ekvationen vi ska lösa är därför för $x = 10 \ cm$:

$0 = \sin(\omega t + \phi - k x)$

Om du däremot tittar på det jag skickade i förra inlägget inser du strax att det räcker att lösa:

$\sin(\omega t +\phi) = 1$

Jag lämnar det till dig att förstå varför.

Tusen tack för hjälpen, tycker att jag förstår mig på vågor lite bättre nu. Blev riktigt förvirrad då boken gav ett konstigt lösningstips.