Vad säger andraderivatan om grafen?
Hej! Jag förstår att jag med hjälp av andraderivatan kan se om en extrempunkt är en maximi -eller minimipunkt. Men säger den någonting om övriga punkter? Jag fick nämligen en fråga om "för vilka x-värden f″(x)>0" tillsammans med en graf för en tredjegradsfunktion med en maximipunkt där x=3 och en minimipunkt där x=-3.
Jag vet då att f''(x)>0 då x=3 men kan jag utläsa någonting mer? Kan jag analysera lutning eller något liknande i fler punkter än extrempunkter med andraderivatan?
Jadå, andraderivatan gör mer än att bara beskriva extrempunkters karaktär! I korthet: andraderivatan beskriver derivatans förändringshastighet, dvs. om derivatan ökar eller minskar. Om andraderivatan är positiv, innebär det att derivatan ökar, och vi har en kurva som går uppåt fortare och fortare, alternativt börjar "vända uppåt":
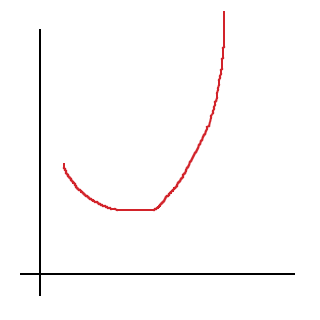
(andraderivatan är positiv i hela intervallet)
Om andraderivatan är negativ, innebär det att derivatan av funktionen avtar, och funktionen börjar vända nedåt:
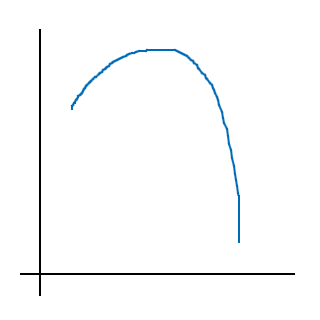
(andraderivatan är här negativ i hela intervallet)
Okej, så om jag sätter in ett x värde i andraderivatans formel och då får ett positivt värde så vet jag att lutningen är positiv där. Så det är alltså likadant som med förstaderivatan där ett positivt värde också innebär positiv lutning?
Aster skrev:Okej, så om jag sätter in ett x värde i andraderivatans formel och då får ett positivt värde så vet jag att lutningen är positiv där. Så det är alltså likadant som med förstaderivatan där ett positivt värde också innebär positiv lutning?
Nej, det en positiv andraderivata säger att förstaderivatan är ökande.
Aster skrev:Okej, så om jag sätter in ett x värde i andraderivatans formel och då får ett positivt värde så vet jag att lutningen är positiv där. Så det är alltså likadant som med förstaderivatan där ett positivt värde också innebär positiv lutning?
Det beror på vad du menar med "lutningen". Vilken lutning?
Använd begreppen f(x), f'(x) och f''(x).
Om vi t.ex. säger att f''(2) > 0, vad vet du då om f(2) och f'(2)?
Yngve skrev:Aster skrev:Okej, så om jag sätter in ett x värde i andraderivatans formel och då får ett positivt värde så vet jag att lutningen är positiv där. Så det är alltså likadant som med förstaderivatan där ett positivt värde också innebär positiv lutning?
Det beror på vad du menar med "lutningen". Vilken lutning?
Använd begreppen f(x), f'(x) och f''(x).
Om vi t.ex. säger att f''(2) > 0, vad vet du då om f(2) och f'(2)?
Om jag hade vetat att kurvan hade en extrempunkt där x=2 så innebär det i alla fall att det är en minimipunkt om f''(2)>0. Men om jag nu inte skulle ha haft någon sån information utan enbart den informationen du gav mig nu så vet jag inte riktigt men jag kan ju gissa. Om f''(2)>0 så kanske det innebär att f'(2)>0, dvs att förändringshastigheten är positiv i punkten. Men jag vet faktiskt inte. vet inte heller vad det säger om f(2).
Smaragdalena skrev:Aster skrev:Okej, så om jag sätter in ett x värde i andraderivatans formel och då får ett positivt värde så vet jag att lutningen är positiv där. Så det är alltså likadant som med förstaderivatan där ett positivt värde också innebär positiv lutning?
Nej, det en positiv andraderivata säger att förstaderivatan är ökande.
Men var det inte det jag sa? Förstår inte riktigt.
Aster skrev:Smaragdalena skrev:Nej, det en positiv andraderivata säger att förstaderivatan är ökande.Men var det inte det jag sa? Förstår inte riktigt.
Det kanske var det du menade, men det var inte det du skrev.
Du skrev:
Okej, så om jag sätter in ett x värde i andraderivatans formel och då får ett positivt värde så vet jag att lutningen är positiv där.
Du skrev inte vilken lutning som är positiv där. Lutningen på f(x)? Lutningen på f'(x)? Lutningen på f''(x)?
Vi kan gissa vad det är du menar, men tänk om du menar en sak och vi gissar en annan. Då kommer vi att ge dig fel svar.
Därav min följdfråga.
Bra begrepp i sammanhanget är "konvex funktion" och "konkav funktion".
Smutstvätt skrev:Jadå, andraderivatan gör mer än att bara beskriva extrempunkters karaktär! I korthet: andraderivatan beskriver derivatans förändringshastighet, dvs. om derivatan ökar eller minskar. Om andraderivatan är positiv, innebär det att derivatan ökar, och vi har en kurva som går uppåt fortare och fortare, alternativt börjar "vända uppåt":
(andraderivatan är positiv i hela intervallet)
Om andraderivatan är negativ, innebär det att derivatan av funktionen avtar, och funktionen börjar vända nedåt:
(andraderivatan är här negativ i hela intervallet)
Men om andra derivatan blir noll vad betyder då? Är det då punkten kallas där för inflektionspunkten? I den punkten lutningen ändras.





