Vad kallas/betyder denna integralnotation?
Halloj!
Jag har sett en typ av integralnotation (särskilt i samband med när man definierar Lebesgueintegraler) som jag inte hade sett tidigare. Den ser ut typ så här:
Vad innebär det när man skriver symbolen för de reella talen under integralen? Kan man skriva andra mängder där också?
Jag skulle säga att det betyder att man integrerar över hela reella tallinjen. Och att det går att skriva andra mängder där också. Det går också bra att i flerdimensionella fallet ha ett antal integraltecken och sedan skriva nedsänkt en beteckning för ett område, för att säga att man integrerar över hela området
Jaha okej, så det är helt enkelt ett annat sätt att skriva integralen nedan?
Låt säga att man hade en mängd . Hade då följande gällt?
Japp på båda punkterna! ^_^
När du läser flervariabelanalys kommer du precis som Hondel säger stöta på situationer där du vill integrera över områden som inte går att beskriva som intervall, rektanglar eller produkter av intervall, och så skriver man helt enkelt integrationsområdet under integralen.
Jag måste förresten passa på att göra reklam för en av mina absoluta favoritsatser inom differentialgeometri: Gauss–Bonnets sats, som säger att den av en yta utan kant enbart beror på ytans , och alltså är invariant under kontinuerliga deformationer!
Med hjälp av integralnotationen som vi har diskuterat här kan man uttrycka detta som att
där är kurvaturfunktionen som mäter hur mycket ytan böjer sig iväg från sitt tangentplan i varje punkt (den är positiv om hela ytan böjer sig inåt under tangentplanet vid punkten, och negativ om ytan böjer sig både inåt och utåt från tangentplanet vid punkten), och är ett berömt topologiskt tal som kallas för ytanas eulerkarakteristik.
Det finns mycket att säga om eulerkarakteristiken, men för begränsade ytor utan kant är den helt enkelt lika med 2−2×(antalet hål), där en sfär anses ha noll hål (och därför eulerkarakteristik 2), medan en torus/"donut" anses ha ett hål (och därför eulerkaraktertisk 0).
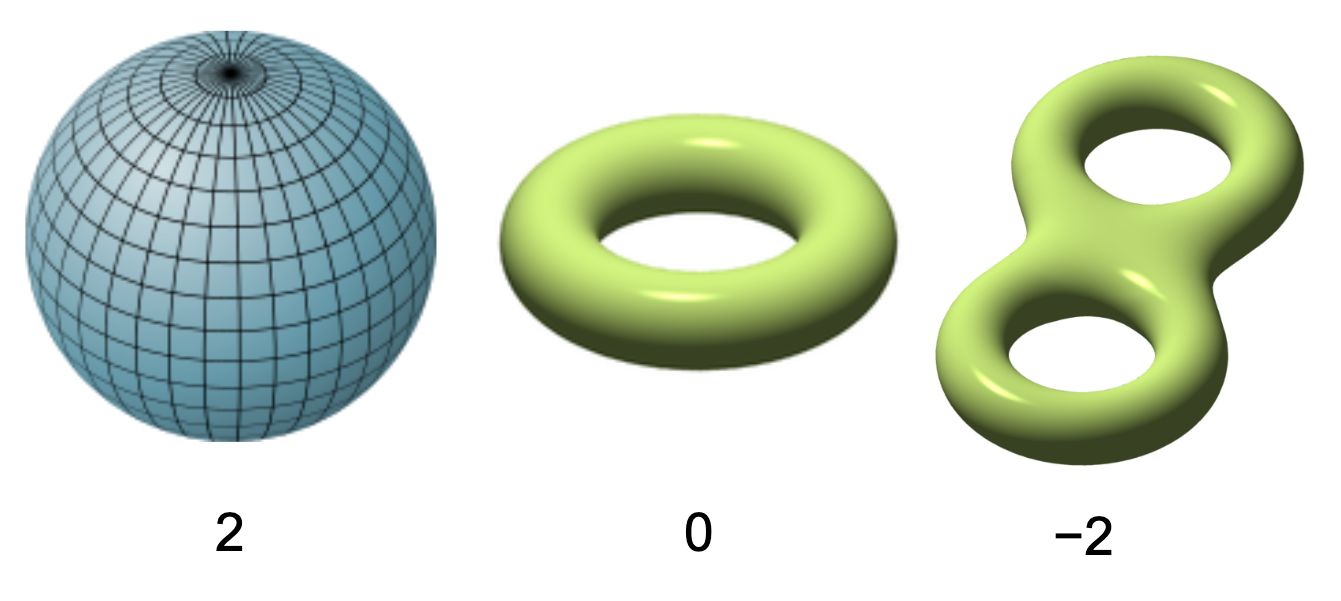 För en sfär med radien är kurvaturfunktionen konstant lika med för alla punkter, vilket ger att integralen i vänsterledet är (total ytarea)×1/r2=4πr2×1/r2=4π, vilket också är precis vad högerledet säger.
För en sfär med radien är kurvaturfunktionen konstant lika med för alla punkter, vilket ger att integralen i vänsterledet är (total ytarea)×1/r2=4πr2×1/r2=4π, vilket också är precis vad högerledet säger.
Poängen med satsen är att detta tal kommer förbli konstant oavsett hur vi kontinuerligt deformerar sfären, eftersom sådana deformationer inte påverkar eulerkarakteristiken. Om vi t.ex. försöker skrynkla ihop den så att den på något ställe blir mer böjd, så kommer den oundvikligen att behöva bli mer platt eller negativt kurvig på något annat ställe för att kompensera för detta.
För en torus tar områdena med positiv kurvatur precis ut områdena med negativ kurvatur (se figuren nedan) oavsett hur man deformerar den.

Här finns två trevliga podcastavsnitt med matematiker som har just Gauss–Bonnet som sin favoritsats:
https://www.scientificamerican.com/blog/roots-of-unity/jeanne-clellands-favorite-theorem/
https://kpknudson.com/my-favorite-theorem/2019/12/11/episode-49-edmund-harriss
Det här låter väldigt intressant! Har du några tips på böcker som behandlar differentialgeometri (för någon som aldrig hållit på med området innan)?
Det är en bra sats om man vill bevisa att trianglar har vinkelsumman 180 grader.
Jag gillar Differential Geometry of Curves and Surfaces av Kristopher Tapp, som i stort sett bara kräver att man har läst flervariabelanalys.
Då ska jag kolla in den efter min kurs i flervarre!




