Vad innebär spänningsfall?
Min lärare förklarade det som att spänningen innan en resistor i en krets var annorlunda än spänningen efter, men samtidigt menar han att spänning är konstant över hela kretsen. Jag fattar ingenting...
Rent logiskt sätt förstår jag inte heller hur en spänning kan vara konstant över en krets. Som jag förstår det är spänning skillnaden i potential mellan två punkter, men den skillnaden minskar ju när laddningarna rör sig genom kretsen...
Jag skulle uppskatta lite förtydliganden!
Det kanske borde heta "potentialfall" men alla säger spänningsfall. Och det är då spänningen över resistorn.
Så potentialen i punkten innan resistorn är alltså högre än potentialen efter resistorn?
Om så är fallet, vad är ens poängen med att konstatera det? Det är väl klart den är, eller? Potentialen minskar väl hela tiden när strömmen rör sig mot minuspolen?
naytte skrev:Så potentialen i punkten innan resistorn är alltså högre än potentialen efter resistorn?
Om så är fallet, vad är ens poängen med att konstatera det? Det är väl klart den är, eller? Potentialen minskar väl hela tiden när strömmen rör sig mot minuspolen?
Ja, och det kan man ha stor nytta av, när man räknar.
naytte skrev:
Rent logiskt sätt förstår jag inte heller hur en spänning kan vara konstant över en krets.
Tänk på KVL. :)
Dracaena skrev:
Tänk på KVL. :)
I mina anteckningar har jag skrivit ned en av Kirchhoffs lagar som "Summan av alla spänningsfall i en krets är 0".
Det innebär väl inte att själva spänningen är konstant över hela kretsen, utan att fallen av spänning mellan alla punkter blir lika stor som spänningen batteriet levererar, eller? Det vill säga spänningen kan (och kommer) vara större ju närmare pluspolen man kommer?
Spänningen från en spänningskälla fördelar ju sig över alla komponenter. Har du 30V men får endast ut 26.53V så fördelas ju detta fortfarande ut till komponenterna. Antag då att kretsen inte kräver 30V eller att vi tar sönder någon komponent.
Jag tror jag först måste reda ut vad spänning faktiskt är för någonting för det verkar inte som jag förstår. Som jag förstår det är spänning skillnaden i den energi som krävs för att flytta en Coulumbs laddning mellan två punkter, det vill säga skillnaden i potential mellan de två punkterna. I en krets mäts potentialen mellan pluspolen och minuspolen.
Om ett batteri levererar krävs för att flytta en laddning mellan pluspolen och minupolen. Men ju närmare minuspolen man kommer, desto mindre energi kommer krävas, eller hur?
Utifrån denna definition av spänning förstår jag inte hur spänning kan "fördela sig". Föreställ dig följande krets med tre utmärkta punkter:
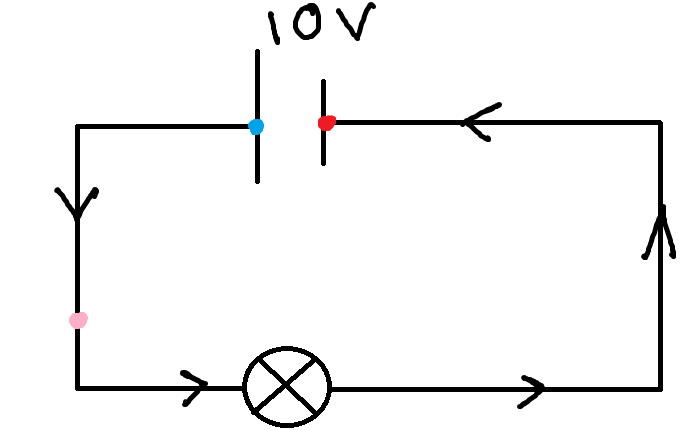
Skillnaden i elektrisk potential mellan den blå och röda punkten kommer vara större än skillnaden i elektrisk potential mellan den rosa och röda, eller hur? Hur kan spänning alltså vara något som "fördelar" sig? En spänning är väl ingen sak, snarare ett mått på skillnad i elektrisk potential?
Om man kan räkna med att resistansen i ledningarna är försumbar, så har den rosa och den blå pricken samma potential. Här finns det ingenting spänningen kan fördela sig mellan, det är ju bara en enda glödlampa som "äter upp" hela spänningen. Spänningsfallet över glödlampan är lika stor som spänningsökningen i batteriet.
Och exakt där är kruxet i vad jag inte förstår. Varför är potentialen lika stor i båda punkterna? Den borde väl minska ju närmare minuspolen man kommer, eller hur? Ju närmare minuspolen den kommer desto mindre elektrisk potentiell energi får laddningarna.
Om resistansen i ledningarna är så stor att man inte kan strunta i den, så har du alldeles rätt (men då har man monterat in alldeles för dåliga ledningar!). Du har ju att U = RI och om R = 0 så blir U lika med noll, och spänningsfallet blir 0.
Om vi istället för en krets föreställer oss ett batteri inkopplat i sig själv:
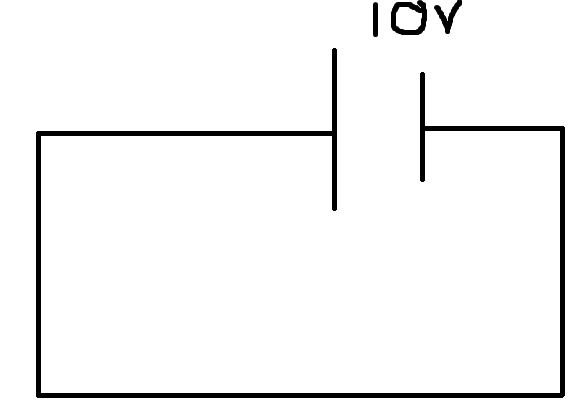
Potentialen "i" minuspolen kommer då vara , eller hur? Men om vi tänker oss en punkt väldigt nära minuspolen, skulle den elektriska potentialen där vara då? Det vill säga potentialen går från 10 till 0 precis i punkten där strömmen når minuspolen?
Om du kortsluter ett batteri kommer det att gå jättemycket ström genom ledningen - om resistansen hade varit 0 skulle strömmen ha varit oändlig. Oändligheter är svåra att räkna på. Om vi inte kan försumma resistansen så kommer ledningens resistans att "äta upp" hela spänningen, precis som lampan i ditt inlägg #8.
Nu är det förståeligt att du ritar upp kretsen för förståelse men vill bara påpeka att du aldrig ska göra så irl. Att kortsluta ground och den positiva terminalen brukar leda till att komponenter smälter eller börjar brinna.
Det kanske underlättar om du introducerar ground vilket i princip alla kretsar har?
Jag tror också att du ska skita i den definitionen av spänning.
Så här fick jag lära mig det på universitet:
tänk dig att du har en vattenslag där vatten rinner ut. Du kan se diametern av slagen som strömmen medan flödet eller "kraften" som trycker vattnet genom slangen med en viss hastighet är spänningen. På så sätt är det inte konstigt att spänningen är fördelad. Olika mycket vatten kommer rinna ut ur slagnarna beroende på trycket och diametern av slangen. men det totala flödet kommer vara densamma. Dvs, totala mängden vatten som runnit ut är av samma magnitud som vattnet som vi började med.
Om du har ett rör och jag häller 2L vatten från ovansidan så kommer in = ut. Sedan kan man börja ta in andra lagar exempelvis conservation of energy osv men det blir nog överflödigt (no pun intended, så klart.). :)
En orsak till begreppsförvirringen här är nog att man ofta pratar om elledningar "utan motstånd".
Sådana finns ju inte. Hur grova kopparkablar man än har, så har de ändå någon milliOhms, mikroOhms eller nanoOhms resistans. Men om man då kopplar kablarna mellan komponenter som har hundratals eller tusentals Ohm resistans, brukar man säga att kablarna har noll resistans.
Börjar man då räkna på spänningsskillnader mellan olika punkter i en sådan kabel, så blir det extremt små spänningsskillnader. Därför säger man att det är samma potential i blå punkt som i rosa punkt ovan.
Om man kortsluter en spänningskälla så händer ungefär en av två saker:
* ledningen blir så varm av den höga strömmen att den smälter eller börjar brinna
* spänningskällan börjar brinna eller exploderar, eller i bästa fall bara tar slut
Om spänningskällan är en dyr apparat så har den nog en säkring som går.
Om den är ett vanligt batteri gissar jag att det bara tar slut, men jag rekommenderar inte att prova inomhus.
naytte skrev:Jag tror jag först måste reda ut vad spänning faktiskt är för någonting för det verkar inte som jag förstår.
Jag gillar liknelsen med värme. Om du tänker dig en vägg där det är kallare på ena sidan väggen så kommer det gå ett värmeflöde genom väggen. Hur stort flödet blir bestäms av temperaturskillnaden och väggens isolering.
Analogin blir då att temperaturskillnaden motsvarar skillnaden i elektrisk potential (spänningen), isoleringen motsvarar resistansen medan värmeflödet motsvarar strömmen.







