Vad blir fel här? Beräkna brytnings index vätska.
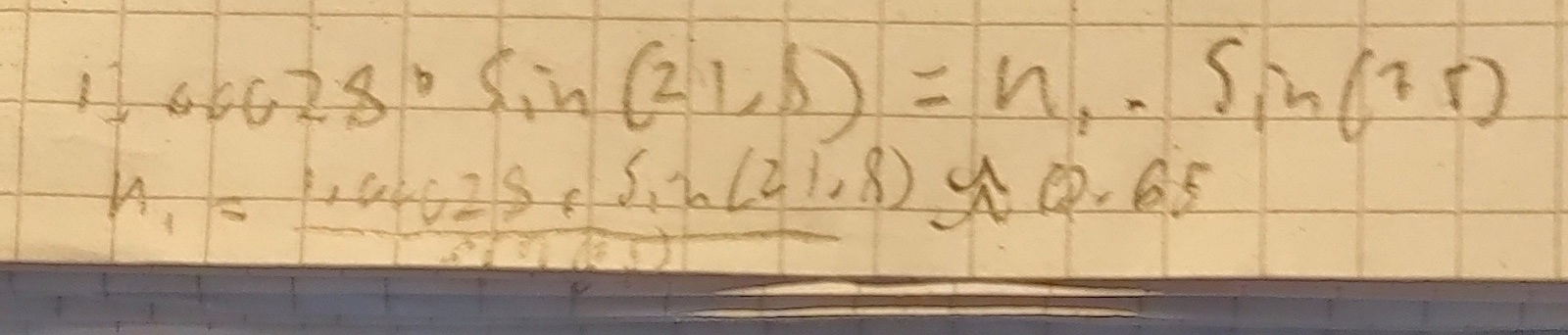
Där den otydligt skrivna vinkeln är 35 grader, dvs nämnaren i kvoten.
Hej.
Kan du rita i figuren vilka vinklar du använder?
Då klarnar det nog förhoppningsvis.
Ta gärna med mer av uppgiften så att vi ser vad kärleks höjd är.
Yngve skrev:Hej.
Kan du rita i figuren vilka vinklar du använder?
Då klarnar det nog förhoppningsvis.
Ta gärna med mer av uppgiften så att vi ser vad kärleks höjd är.
Den osynliga höjden är 10 cm.
OK bra.
Tänk på att infalls- och brytningsvinkeln räknas mot gränsytans normal, dvs den streckade linjen och dess förlängning neråt.
Yngve skrev:OK bra.
Tänk på att infalls- och brytningsvinkeln räknas mot gränsytans normal, dvs den streckade linjen och dess förlängning neråt.
Oj jag såg det nu, vinkeln höger om i är den rätta alltså? Mot normalen, rätt räkmat på vänster sida om vätskan men ej till höger. Tack återigen!
Tillägg: 22 okt 2023 15:24
I=90-35
?
AlexanderJansson skrev:
Oj jag såg det nu, vinkeln höger om i är den rätta alltså? Mot normalen, rätt räkmat på vänster sida om vätskan men ej till höger. Tack återigen!
Jag förstår inte vad du menar.
Infallsvinkeln i, dvs vinkeln I vätskan, är korrekt beskriven, men brytningsvinkeln b, dvs vinkeln I luften, är inte korrekt beskriven.
Yngve skrev:AlexanderJansson skrev:Oj jag såg det nu, vinkeln höger om i är den rätta alltså? Mot normalen, rätt räkmat på vänster sida om vätskan men ej till höger. Tack återigen!
Jag förstår inte vad du menar.
Infallsvinkeln i, dvs vinkeln I vätskan, är korrekt beskriven, men brytningsvinkeln b, dvs vinkeln I luften, är inte korrekt beskriven.
Arc tan 3/7.5 ger 21.8
Tillägg: 22 okt 2023 15:31
21.8 grader är (b) på bilden
Och (I) borde i själva verket vara 90-35=55 grader.
Sammantaget ger detta mig fel lösning fortfarande.
AlexanderJansson skrev:Arc tan 3/7.5 ger 21.8
Ja, men det är inte brytningsvinkeln.
Brytningsvinkeln ska räknas mot normalen till gränsskiktet, se bild.
Yngve skrev:AlexanderJansson skrev:Arc tan 3/7.5 ger 21.8
Ja, men det är inte brytningsvinkeln.
Brytningsvinkeln ska räknas mot normalen till gränsskiktet, se bild.
Jag använder vinklarna mot gränsikt aj då
Tillägg: 22 okt 2023 15:34
Bör inte jag få rätt svar endå?
Tillägg: 22 okt 2023 15:37
Där vi rotera bilden
AlexanderJansson skrev:
Jag använder vinklarna mot gränsikt aj då
Nej, du använde vinkeln mot normalen som infallsvinkel och vinkeln mot gränsskiktet som brytningsvinkel.
Tillägg: 22 okt 2023 15:34
Bör inte jag få rätt svar endå?
Nej.
Yngve skrev:AlexanderJansson skrev:Jag använder vinklarna mot gränsikt aj då
Nej, du använde vinkeln mot normalen som infallsvinkel och vinkeln mot gränsskikten som brytningsvinkel.
Tillägg: 22 okt 2023 15:34
Bör inte jag få rätt svar endå?
Nej.
Bytte sedan till 90-35
Tillägg: 22 okt 2023 15:39
I= 55(grader)
Och b = 21.8(grader)
AlexanderJansson skrev:
Bytte sedan till 90-35
Du måste visa hela dina uträkningar om du vill ha hjälp att hitta eventuella feltänk/felräkningar.
Yngve skrev:AlexanderJansson skrev:Bytte sedan till 90-35
Du måste visa hela dina uträkningar om du vill ha hjälp att hitta eventuella feltänk/felräkningar.
Men om vi fastslår att de senaste givna vinklarna stämmer, bör inte brytnings lagen där 1.00028*sin(21.8)=n*sin(55) ge rätt svar?
Brytningslagen lyder inte så. Den säger att man ska räkna infalls- och brytningsvinkeln mot normalen, inte mot gränsskiktet.
Men du undrar alltså om det går bra att räkna även på det sättet, dvs att räkna vinklarna mot gränsskiktet?
I så fall tycker jag att det är en utmärkt idé att du själv kontrollerar om det går.
Alltså:
- Beräkna n ur ekvationen 1,00029*sin(21,8°) = n*sin(55°)
- Beräkna n ur ekvationen 1,00029*sin(68,2°) = n*sin(35°)
- Jämför de två värdena på n.
Är de lika stora?
Om nej så spelar det tydligen roll hur man väljer vinklar.
Yngve skrev:Brytningslagen lyder inte så. Den säger att man ska räkna infalls- och brytningsvinkeln mot normalen, inte mot gränsskiktet.
Men du undrar alltså om det går bra att räkna även på det sättet, dvs att räkna vinklarna mot gränsskiktet?
I så fall tycker jag att det är en utmärkt idé att du själv kontrollerar om det går.
Alltså:
- Beräkna n ur ekvationen 1,00029*sin(21,8°) = n*sin(55°)
- Beräkna n ur ekvationen 1,00029*sin(68,2°) = n*sin(35°)
- Jämför de två värdena på n.
Är de lika stora?
Om nej så spelar det tydligen roll hur man väljer vinklar.
Du har rätt, men hur? Det blir inte desamma, min nya fråga är varför jag vanligt vis kan rita normalen vinkel rät mot mediumet, men i denna uppgift inte?
Tillägg: 22 okt 2023 15:58
Denna video genomgång ritar normalen vinkel rät mot mediumet :0
https://www.youtube.com/watch?v=rS6-clCqeRw
AlexanderJansson skrev:Yngve skrev:Brytningslagen lyder inte så. Den säger att man ska räkna infalls- och brytningsvinkeln mot normalen, inte mot gränsskiktet.
Men du undrar alltså om det går bra att räkna även på det sättet, dvs att räkna vinklarna mot gränsskiktet?
I så fall tycker jag att det är en utmärkt idé att du själv kontrollerar om det går.
Alltså:
- Beräkna n ur ekvationen 1,00029*sin(21,8°) = n*sin(55°)
- Beräkna n ur ekvationen 1,00029*sin(68,2°) = n*sin(35°)
- Jämför de två värdena på n.
Är de lika stora?
Om nej så spelar det tydligen roll hur man väljer vinklar.
Du har rätt, men hur? Det blir inte desamma, min nya fråga är varför jag vanligt vis kan rita normalen vinkel rät mot mediumet, men i denna uppgift inte?
Tillägg: 22 okt 2023 15:58
Denna video genomgång ritar normalen vinkel rät mot mediumet :0
https://www.youtube.com/watch?v=rS6-clCqeRw
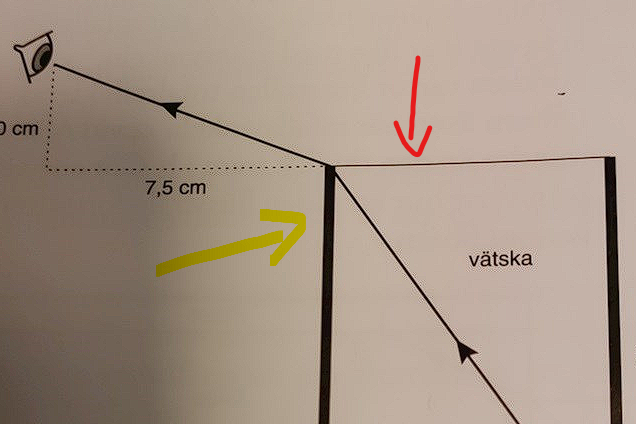Oj jag såg fel, jag trode gränsen till vätskan var gula pilen inte röda, ursäkta. Detta är ett förekomande problem för mig i uppgifter, spelar ingen roll hur länge jag tittar och läser om uppgiften, jag ser fel på åter bara.
Men tackvare din figur fick du mig att inse att det måste vara vätskan, jag stirra mig blint på min uppritade figur.
OK bra.
Har du någon obesvarad fråga eller fundering då?
Yngve skrev:OK bra.
Har du någon obesvarad fråga eller fundering då?
Är det besvärligt när jag läser eller ser uppgifter fel? Om du någon gång mosstänker det, så hojta till, det är ett vanligt förekomande problem för mig.
AlexanderJansson skrev:
Är det besvärligt när jag läser eller ser uppgifter fel?
Det är besvärligt för dig, inte för oss.
Om du någon gång mosstänker det, så hojta till, det är ett vanligt förekomande problem för mig.
OK, om du hjälper till genom att tydligt beskriva hur du tolkar uppgiften.
Då hittar vi de situationerna snabbare.
