Vad är sannolikheten att totala poöngsumman blir mer än 4?
Hej! Jag försökte lösa denna fråga men fick 0,3 som svar medan facit säger 0,4, vet inte riktigt vad jag gör fel?:(

Facit:
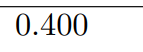
Mi
Tack på förhand!
Du räknar lite fel när du räknar ut fördelningen för xi.
Exemeplvis. Om xi är 1 betyder det att summan av xi1 och xi2 är 1. Det sker när antingen xi1 = 1 och xi2=0, ELLER när xi1 = 0 och xi2=1.
Att räkna ut fullständiga fördelningen för xi är nog lite jobbigt. Det är nog enklare att bara räkna ut sannolikheterna för att xi är 5 och 6 (som är de alternativ då xi är större än 4). Xi kan som störst anta 6 eftersom xi1 och xi2 kan vara max 3, och därmed blir summan som störst 6.
Hondel skrev:Du räknar lite fel när du räknar ut fördelningen för xi.
Exemeplvis. Om xi är 1 betyder det att summan av xi1 och xi2 är 1. Det sker när antingen xi1 = 1 och xi2=0, ELLER när xi1 = 0 och xi2=1.Att räkna ut fullständiga fördelningen för xi är nog lite jobbigt. Det är nog enklare att bara räkna ut sannolikheterna för att xi är 5 och 6 (som är de alternativ då xi är större än 4). Xi kan som störst anta 6 eftersom xi1 och xi2 kan vara max 3, och därmed blir summan som störst 6.
Ah okej tack! Jag vet dock inte hur jag ska få fram p(xi=5) och p(xi=6). Jag tänker att Det finns 2 sätt som xi kan bli 5 på (xi1=2 &xi2=3 eller xi1=3 &xi2=2) så antalet gynsamma utfall är 2? och antalet möjliga är 4^2? Så vi får p(xi=5) = 2/4^2 = 0,125
Det finns endast 1 sätt att p(xi=6) (om xi1=3 & xi2=3) så antalet gynsamma utfall är 1 och antalet möjliga är fortfarande 4^2. så vi får p(xi=6) = 1/16=0,0625
Vi får att p(xi>=4) = p(xi =5)+p(xi=6) = 0,125+0,0625 = 0,18275
Detta stämmer dock inte med facit:(
Du har helt rätt i att det finns tre möjligheter. Antingen 3+3=6 eller 2+3=5 eller 3+2=5. Men sen blir det konstigt i din uträkning.
För att få utfallet 6 måste Olle kasta först en 3:a (sannolikhet 0.4) och sedan en 3:a till (sannolikhet 0.4).
Sannolikheten att Olle ska lyckas med två 3:or på raken är alltså
Kan du på liknande sätt räkna ut sannolikheten för ?
D4NIEL skrev:Du har helt rätt i att det finns tre möjligheter. Antingen 3+3=6 eller 2+3=5 eller 3+2=5. Men sen blir det konstigt i din uträkning.
För att få utfallet 6 måste Olle kasta först en 3:a (sannolikhet 0.4) och sedan en 3:a till (sannolikhet 0.4).
Sannolikheten att Olle ska lyckas med två 3:or på raken är alltså
Kan du på liknande sätt räkna ut sannolikheten för ?
Ah okej! Men jag blir osäker hur man ska göra då han för att få 5 kan det ske på 2 sätt så man kan väll inte säga att
P(xi=5) = 0,3*0,4 = 0,12
?
det finns två alternativ. Xi1=2 och Xi2=3, eller Xi1=3 och Xi2=2. Kan du räkna ut sannolikheterna för de två alternativen? Hur kan du kombinera dessa?
Hondel skrev:det finns två alternativ. Xi1=2 och Xi2=3, eller Xi1=3 och Xi2=2. Kan du räkna ut sannolikheterna för de två alternativen? Hur kan du kombinera dessa?
P(xi1 = 2,xi2=3) = P(xi1=3,xi2=2) = 0,3*0,4 = 0,12
vi måste välja 1 av två kombinationer:
?
Du ska summera dessa sannolikheter.
Tänk att A är händelsen att xi1=2 och xi2=3, och B är händelsen att xi1=3 och xi2=2. Då är P(xi=5)=P(A union B) = P(A) + P(B) -P(A snitt B) = P(A) + P(B) eftersom A och B kan inte ske samtidigt och därför är P(A snitt B)=0.
Hondel skrev:Du ska summera dessa sannolikheter.
Tänk att A är händelsen att xi1=2 och xi2=3, och B är händelsen att xi1=3 och xi2=2. Då är P(xi=5)=P(A union B) = P(A) + P(B) -P(A snitt B) = P(A) + P(B) eftersom A och B kan inte ske samtidigt och därför är P(A snitt B)=0.
Ah okej det är sannt tack! Men även om jag ska addera P(A)+P(B) så måste jag beräknat deras individuella sannolikheter fel efter som jag fick fram att P(A)=P(B)=0,12 så vi får P(A)+P(B)=0,12+0,12 = 0,24 Men svaret är 0,4:(
Du har räknat rätt, det blir 0.24. Men det finns ju också möjligheten att Olle får 3+3 poäng. Vad är sannolikheten för det? Och vad blir den totala sannolikheten då?
Du har alltså tre utfall
Du har beräknat
Tillägg: 20 jul 2024 16:27
Ska som påpekat naturligtvis vara
D4NIEL skrev:Du har räknat rätt, det blir 0.24. Men det finns ju också möjligheten att Olle får 3+3 poäng. Vad är sannolikheten för det? Och vad blir den totala sannolikheten då?
Du har alltså tre utfall
Du har beräknat
Ja det är sant! Visst menar du xi1=3, xi2=3 på C?
Tack så mycket nu blev det rätt:)
p(xi>4) = p(xi=5) + p(xi = 6) = p(xi1=2,xi2=3) + p(xi1=3,xi2=2) + p(xi1=3,xi2=3) = 0,3*0,4 + 0,3*0,4 + 0,4^2 = 0,4
Hejhej! skrev:Hondel skrev:Du ska summera dessa sannolikheter.
Tänk att A är händelsen att xi1=2 och xi2=3, och B är händelsen att xi1=3 och xi2=2. Då är P(xi=5)=P(A union B) = P(A) + P(B) -P(A snitt B) = P(A) + P(B) eftersom A och B kan inte ske samtidigt och därför är P(A snitt B)=0.Ah okej det är sannt tack! Men även om jag ska addera P(A)+P(B) så måste jag beräknat deras individuella sannolikheter fel efter som jag fick fram att P(A)=P(B)=0,12 så vi får P(A)+P(B)=0,12+0,12 = 0,24 Men svaret är 0,4:(
Nu har det ju löst sig, men min förklaring var då alltså bara att räkna ut sannolikheten för att xi=5. Som du sen såg behöver du även sannolikheten för att xi=6 för att kunna räkna ut sannolikheten att xi>4
Hondel skrev:Hejhej! skrev:Hondel skrev:Du ska summera dessa sannolikheter.
Tänk att A är händelsen att xi1=2 och xi2=3, och B är händelsen att xi1=3 och xi2=2. Då är P(xi=5)=P(A union B) = P(A) + P(B) -P(A snitt B) = P(A) + P(B) eftersom A och B kan inte ske samtidigt och därför är P(A snitt B)=0.Ah okej det är sannt tack! Men även om jag ska addera P(A)+P(B) så måste jag beräknat deras individuella sannolikheter fel efter som jag fick fram att P(A)=P(B)=0,12 så vi får P(A)+P(B)=0,12+0,12 = 0,24 Men svaret är 0,4:(
Nu har det ju löst sig, men min förklaring var då alltså bara att räkna ut sannolikheten för att xi=5. Som du sen såg behöver du även sannolikheten för att xi=6 för att kunna räkna ut sannolikheten att xi>4
Ja nu ser jag förlåt jag hade glömt bort p(xi=6) förut! Tack:)

