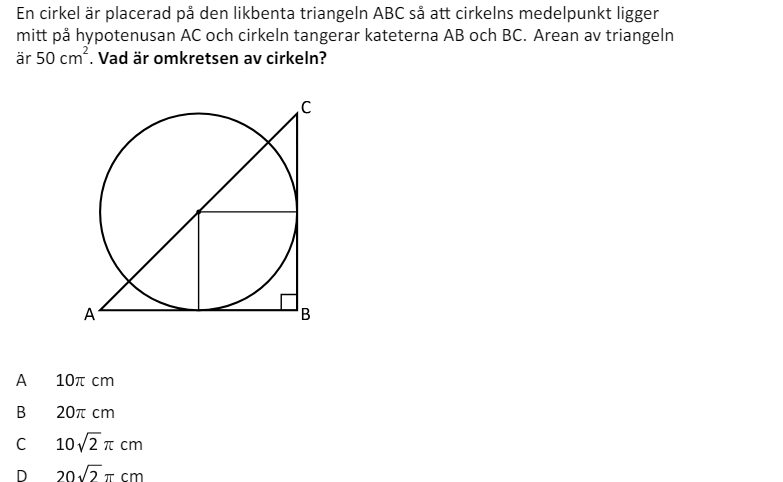
Vad är omkretsen av cirkeln ?
Jag tror meningen med denna uppgift är väl att nyttja Pythagoras sats eller ?
Självklart. Men först, vad blir triangelns sidor?
Du behöver inte använda Pythagoras sats.
För att bestämma triangelns sidlängder kan du istället använda mittpunktsformeln.
Triangelarea = 1/2 2r 2r = 50 <=> r=5
Omkrets = ...
Så alltså är Alternativ A. rättsvar
Ja, det stämmer. Jag löste den själv utan Pythagoras men lyckas ändå svara ja på din fråga. Midsommar är som den är😌
Yngve skrev:Du behöver inte använda Pythagoras sats.
För att bestämma triangelns sidlängder kan du istället använda mittpunktsformeln.
Hur skulle mittpunktsformeln (x1+x2/2,y1+y2/2) kunna användas här ?
Du vet att triangeln ABC har arean cm2.
Triangeln ABC är rätvinklig, vilket betyder att dess area är .
Vi vet att cm2, vilket ger oss att cm2
Eftersom ABC är likbent så är , vilket ger oss att cm2, dvs cm.
Det betyder att och , se bild.

Nu kan du använda mittpunktsformeln för att bestämma koordinaterna för medelpunkten .
Då trollar cirkelns radie ut.
Hej,
Yngve det var ett tag sedan jag postade denna tråd, men undrar ifall du skulle ha använt Trinty:s metod under HP ? Eftersom under provet så gör man det under tidspress och mitt mittpunktsformen skulle väl ta längre tid med beräkningar.
Jag skulle ha tänkt så här:
"Likbent triangel, jag kallar kateternas längder a. Då är triangelns area a2/2. Jag vet att detta är lika med 50 cm2, vilket medför att a2 = 100, vilket medför att a = 10. Cirkelns medelpunkt ligger mitt på hypotenusan, vilket gör att radien måste vara 5 cm. Detta ger oss omkretsen 2pi r, dvs 10 pi."



