vad är fell har? är det 0.5 mm eller 1 mm?
är fel här är 0.5 mm eller 1 mm
jag tror att det är 1 mm eftersom vi jämföra två sida. Dvs att 0,5 mm från höger sida och 0,5 mm från vänster sida eller hur?
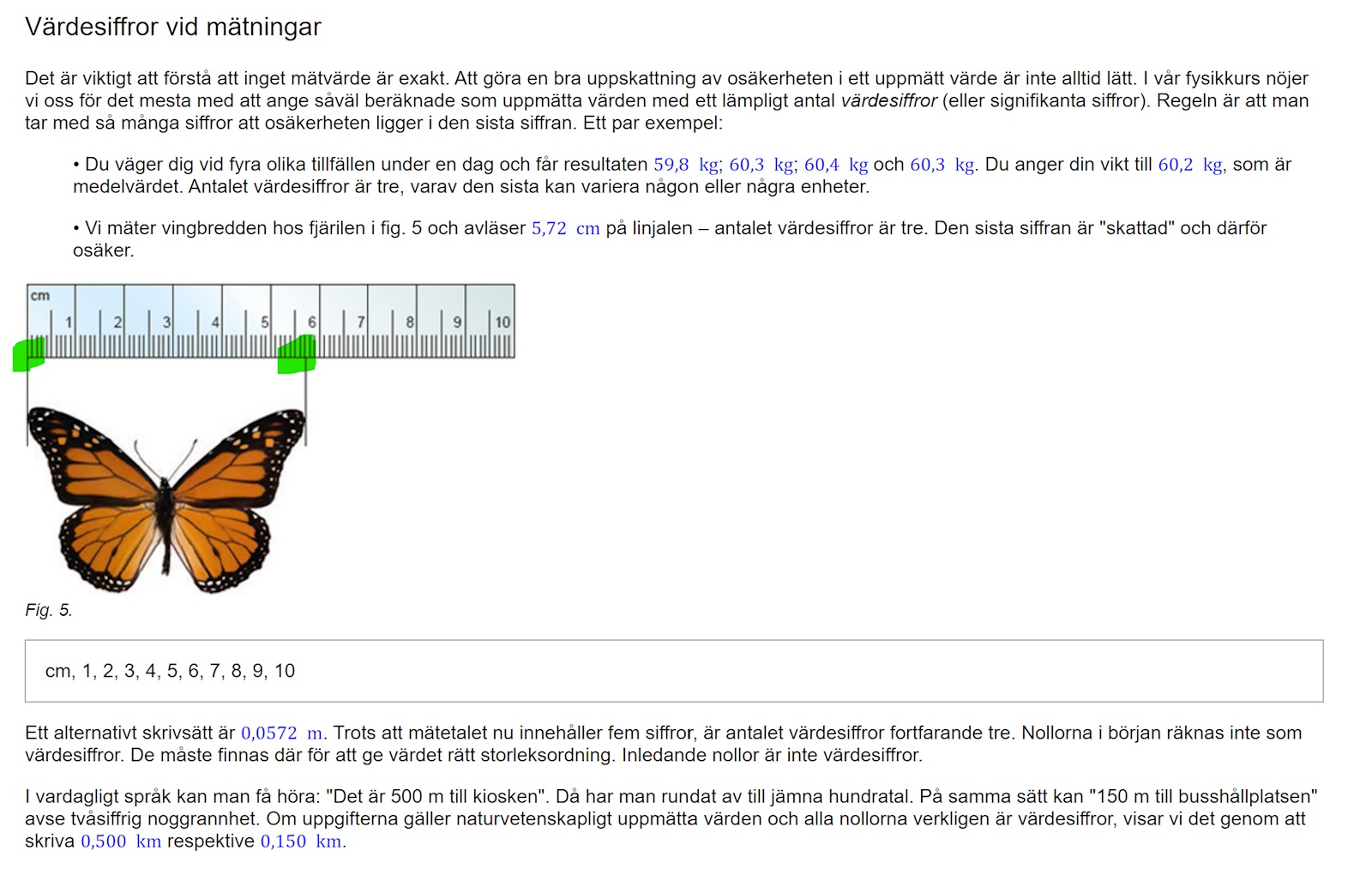
"Vingbredd" är inte bredden på en vinge, utan avståndet mellan vingspetsarna.
Ett bättre ord för samma sak är "vingspann".
Men vad är fel här är det 0.5 mm elle 1 mm
Stephan70707 skrev:jag tror att det är 1 mm eftersom vi jämföra två sida. Dvs att 0,5 mm från höger sida och 0,5 mm från vänster sida eller hur?
Detta låter rimligt.
finns någon kan svara mig om jag rätt 100% snälla? tusen tack!
Jag tycker det är dumt av uppgiftstexten att påstå att vi avläser 5,72 cm på linjalen. Det gör vi inte alls. Vi avläser 5,7 och litet till. Det går inte att säga om det är 5,71 eller 5,73.
Det är visserligen så att man kan avgöra om värdet är nånstans runt 5,72 snarare än runt 5,74, men när det finns streckmarkeringar så använder man bara strecken. Man ska avläsa 5,7 här. Man ser att det inte är 5,6 eller 5,8, och felet är följaktligen plus/minus 0,05, alltså ett spann på 0,1.
Om man verkligen använder ögonmåttet efter bästa förmåga så kan man säga att felet är typ plus/minus 0,1. Så brukade jag göra i skolan, men jag tror inte man ska göra så.
Vänstersidan här har inget fel, man har lagt vingkanten precis vid 0.
men jag hitta den

Laguna skrev:Vänstersidan här har inget fel, man har lagt vingkanten precis vid 0.
Visst, så är det om man mäter något av stål.
Men av någon konstig anledning (estetiska skäl?) valde uppgiften fjärilsvingar. Dessa har ingen längd som man kan bestämma på tiondelar av en millimeter.
Stephan70707 skrev:
när använda den här sätt ?? det lite konstigt för mig att boken inte förklara det tydligt
om ni vill kolla https://www.youtube.com/watch?v=GbnR6QsbE1M
Stephan70707 skrev:
när använda den här sätt ?? det lite konstigt för mig att boken inte förklara det tydligt
Det måste man använda om man kan inte anlägga föremålet till linjalens kant.
Vid ett skjutmått är den ena sidan exakt. Så kan det också vara med stållinjal eller rullmått.
Men linjaler av trä eller plast brukar ha en skala som börjar typ en halv centimeter in.
jag hittar den här i university of mississippi

Det finns ganska många begrepp, mätvärden och fysiska begränsningar i den här diskussionen nu.
Först har vi upplösningen i mätskalan: Det är 1 mm mellan varje streck på linjalen. Ofta säger man då att en avläsning sker mot "närmaste streck", alltså att man anger måttet 5.7 cm därför att mätningen hamnar närmast det streck som visar just 5.7 cm. Då har man i alla fall inte gjort mer fel än ett halvt avstånd mellan strecken, i det här fallet 0.5 mm.
I den här uppgiften har man sett att vingbredden ligger mellan 5.7 och 5.8 cm, och bedömer att bredden är 5.72 cm. Den där tvåan är, som det står i uppgiften, osäker. Ändå verkar man tycka att bredden måste vara närmare 5.72 än 5.71 eller 5.73 cm. I så fall är mätfelet högst 0.005 cm (det är 0.05 mm och inte 0.5 mm som du har skrivit). Man litar väldigt mycket på sina ögon, tycker jag.
Så fort man gör mätningar i verkligheten får man tänka på andra fel man kan göra. Som flera (du också. Bra!) har skrivit så har man i det här fallet inget exakt läge för "noll". Man kan ha placerat vänstra vingspetsen en bit från linjalens nolla, så att vi har ett mätfel där också. Boken verkar inte ha tänkt på det.
Ditt citat från University of Mississippi säger att mätfelet är hälften av linjalens upplösning, hälften av avståndet mellan linjalens streck. Det skulle bli hälften av en millimeter. Nu står det något annat i din bok: att man med ögonen kan se att vingspetsen ligger 0.2 millimeter till höger om 57mm-strecket. Vem har rätt? Det är inte självklart, utan beror på vad man tycker. Hur noga ser man?
Jag förstår att man kan bli förvirrad, när olika böcker säger mot varandra.
Bubo skrev:Ändå verkar man tycka att bredden måste vara närmare 5.72 än 5.71 eller 5.73 cm. I så fall är mätfelet högst 0.005 cm
Nej, det är inget måste. Det är en uppskattning. Någon annan kan avläsa 5,73 cm. Som uppgiften också säger: den sista siffran är osäker.
Felgränsen är större än 0,005 cm. Jag skulle skriva t ex 5,72 ± 0,02 cm.
Det är bedömningar, och en annan kan göra en annan avläsning och en annan bedömning av hur stor felgränsen är.
Folk är inte så vana längre att avläsa en analog skala.
Pieter Kuiper skrev:Bubo skrev:Ändå verkar man tycka att bredden måste vara närmare 5.72 än 5.71 eller 5.73 cm. I så fall är mätfelet högst 0.005 cm
Nej, det är inget måste. Det är en uppskattning. Någon annan kan avläsa 5,73 cm. Som uppgiften också säger: det sista siffran är osäker.
Felgränsen är större än 0,005 cm. Jag skulle skriva t ex 5,72 ± 0,02 cm.
Det är bedömningar, och en annan kan göra en annan avläsning och en annan bedömning av hur stor felgränsen är.
Folk är inte så vana längre att avläsa en analog skala.
Men är det fel att säger att Mätning osäkerheten är 0.5 mm (enligt university of mississippi) eftersom den minsta enhet är 1 mm därmed halv av det 0.5 mm stämmer det?
Bubo skrev:Jag förstår att man kan bli förvirrad, när olika böcker säger mot varandra.
Jaaaa, det konstigt att boken inte förklara det tydligt
och varför det finns många böcker som säger olika sak?
I matematik finns ingen som det och fysik nästan är matematik
Tyvärr finns det inga entydiga regler kring hur man ska hantera och uppskatta mätfel. Tvärtom handlar det oftast om sunt förnuft.
Det viktiga är att man skriver något om hur man uppskattar noggrannheten och att resonemanget man för är tydligt, konsistent och logiskt. Dessutom förväntas man följa ett antal "tumregler" som skiljer sig åt mellan till exempel USA och Europa.
Jag skulle säga att fjärilens vingspann är
D4NIEL skrev:Tyvärr finns det inga entydiga regler kring hur man ska hantera och uppskatta mätfel. Tvärtom handlar det oftast om sunt förnuft.
det lite orättvis, människor kan tänka på olika sätt och det måste finns regler det är naturvetenskap och inte literature. jag kan tänka på ett sätt och mitt lärare kan tänka på annan sätt!!!
Det viktiga är att man skriver något om hur man uppskattar noggrannheten och att resonemanget man för är tydligt, konsistent och logiskt. Dessutom förväntas man följa ett antal "tumregler" som skiljer sig åt mellan till exempel USA och Europa.
Jag skulle säga att fjärilens vingspann är
men som du ser när det kommer till samma fråga (university of mississippi) säger att Mätning osäkerheten är 0.5 mm

Ja, om du vill kan du säga att du när du mäter något med en linjal graderad 1mm kan uppnå en noggrannhet om . Och så kan du hänvisa till att du har en tumregel om att linjalens minsta gradering ska delas med två. Ingen skulle invända mot det om du kan förklara och försvara din ståndpunkt, eftersom det här handlar om tyckande.
Det man kan säga om mätningen är att fjärilen förmodligen är elastisk och enkelt kan bli både 1mm längre och en 1mm kortare beroende på väder och vind och hur man arrangerar den rent praktiskt. Linjalen som kanske är av plast är förmodligen screentryckt och noggrannheten är bland annat beroende på hur många linjaler som trycktes vid tillfället (värmeglidning). Dessutom är mätfelet relativt, inte absolut (ju längre sträck du mäter, desto större fel). När jag började mellanstadiet delades det ut plastlinjaler till klassen. Jag minns att vi jämförde våra nya mätinstrument och noterade att det kunde skilja upp till någon millimeter mellan våra linjaler. Det bekymrade oss inte särskilt eftersom linjalerna ändå skulle gå sönder under fäktning nästföljande rast.
Hursomhelst, en viktig punkt som du tar upp är huruvida fixeringen vid koordinatsystemet sker vid 1 eller 2 punkter, dvs om mätningen egentligen sker vid båda ändarna. Här har faktiskt fysiken ett svar på frågan, det måste registreras två mätvärden (ett i varje ände av mätstaven), och de ska registreras samtidigt i den referensram staven befinner sig i vila.
D4NIEL skrev:Hursomhelst, en viktig punkt som du tar upp är huruvida fixeringen vid koordinatsystemet sker vid 1 eller 2 punkter, dvs om mätningen egentligen sker vid båda ändarna. Här har faktiskt fysiken ett svar på frågan, det måste registreras två mätvärden (ett i varje ände av mätstaven), och de ska registreras samtidigt i den referensram staven befinner sig i vila.
Kan du snälla förklara mer med detaljer?
Jag förstår inte vad menar du med "vid koordinatsystemet sker vid 1 eller 2 punkter" och "det måste registreras två mätvärden (ett i varje ände av mätstaven), och de ska registreras samtidigt i den referensram staven befinner sig i vila."
Tusen tack!
Stephan70707 skrev:[...] men som du ser när det kommer till samma fråga (university of mississippi) säger att Mätning osäkerheten är 0.5 mm
Ja, man kan säga att noggrannheten är hälften av upplösningen. Man kan säga att man hittar närmaste millimeterstreck, så att felet maximalt är 0.5 mm.
Det man har gjort i din bok är att bedöma hur långt från millimeterstrecket mätningen är (i det här fallet 0.2 millimeter, så att man bedömer vingbredden till 57.2 millimeter. Så kan man göra, men University of Mississippi skulle säga att mätningen är ungefär 57 millimeter, inte 56 och inte 58.
"En eller två punkter": Så som man har mätt här kan man inte vara säker på att den ena vingspetsen ligger precis på linjalens nolla. Man bör ta hänsyn till att det kan bli ett fel där också. (Det verkar din bok inte ha tänkt på).
Bubo skrev:Stephan70707 skrev:[...] men som du ser när det kommer till samma fråga (university of mississippi) säger att Mätning osäkerheten är 0.5 mm
Ja, man kan säga att noggrannheten är hälften av upplösningen. Man kan säga att man hittar närmaste millimeterstreck, så att felet maximalt är 0.5 mm.
Det man har gjort i din bok är att bedöma hur långt från millimeterstrecket mätningen är (i det här fallet 0.2 millimeter, så att man bedömer vingbredden till 57.2 millimeter. Så kan man göra, men University of Mississippi skulle säga att mätningen är ungefär 57 millimeter, inte 56 och inte 58.
jag tror att University of Mississippi ska säger att det är
stämmer det??
"En eller två punkter": Så som man har mätt här kan man inte vara säker på att den ena vingspetsen ligger precis på linjalens nolla. Man bör ta hänsyn till att det kan bli ett fel där också. (Det verkar din bok inte ha tänkt på).
men vad menar D4NIEL med "och de ska registreras samtidigt i den referensram staven befinner sig i vila"
Är alltid det halv av den minsta enhet som verktyg har oavsett om vi jämför tvåsidig eller en sida spelar det ingen roll?????
Ju fler mätningar (observationer) du gör, desto större osäkerhet. Om du mäter två punkter kan du addera osäkerheterna.
Eftersom fjärilens läge till vänster inte är fixerat vid linjalens nolla måste du anse att också den avläsningen är behäftad med ett mätfel. Jag skulle därför säga att du har ett avläsningsfel i båda ändarna.
Vidare brukar man skilja på "avläsningsfel" och mätinstrumentets noggrannhet, men det blir snabbt ogörligt om man försöker göra en stringent särskiljande definition. Praktiskt sett kan man ju lägga något mot något annat och implicit anse att ena ändpunkten är fixerad, men det i sig kräver en fixering av koordinatsystemet. Naturligtvis är även skjutmått behäftade med flera olika mätfel, trots att "båda ändar" är "fixerade.

Som du märker finns det inga exakta svar här, utan man får göra uppskattningar av felkällor så gott man kan. Däremot är vad som menas med en längd av något väldefinierat i teoretisk fysik

Längden av sträckan (A, B) mäts genom att man observerar rumskoordinaterna för punkten A och B (två mätningar som utförs samtidigt). Sedan bildar skillnaden definitionsmässigt en längd. Teoretiskt sett kan man kan alltså aldrig mäta en längd utan att på något sätt ha gjort två samtidiga observationer (två samtidiga händelser).
D4NIEL skrev:Ju fler mätningar (observationer) du gör, desto större osäkerhet. Om du mäter två punkter kan du addera osäkerheterna.
Eftersom fjärilens läge till vänster inte är fixerat vid linjalens nolla måste du anse att också den avläsningen är behäftad med ett mätfel. Jag skulle därför säga att du har ett avläsningsfel i båda ändarna.
Vidare brukar man skilja på "avläsningsfel" och mätinstrumentets noggrannhet, men det blir snabbt ogörligt om man försöker göra en stringent särskiljande definition. Praktiskt sett kan man ju lägga något mot något annat och implicit anse att ena ändpunkten är fixerad, men det i sig kräver en fixering av koordinatsystemet. Naturligtvis är även skjutmått behäftade med flera olika mätfel, trots att "båda ändar" är "fixerade.
Som du märker finns det inga exakta svar här, utan man får göra uppskattningar av felkällor så gott man kan. Däremot är vad som menas med en längd av något väldefinierat i teoretisk fysik
Längden av sträckan (A, B) mäts genom att man observerar rumskoordinaterna för punkten A och B (två mätningar som utförs samtidigt). Sedan bildar skillnaden definitionsmässigt en längd. Teoretiskt sett kan man kan alltså aldrig mäta en längd utan att på något sätt ha gjort två samtidiga observationer (två samtidiga händelser).
Om jag förstår rätt ! det kan bli fel i början av linjal och i ände av linjal som mitt bild visar därmed osäkerheten här kommer bli 1 mm.
men samtidigt University of Mississippi säger att osäkerheten är halv av den minsta enhet som verktyg (0.5 mm)?
Varför det finns skillnad???
Är det fel att säger Osäkerhet i mätningar är alltid halv av den minsta enhet som verktyg har oavsett om vi jämför tvåsidig eller en sida spelar det ingen roll ( som University of Mississippi )
tusen tack för er hjälp!







