Uttryck vektor med diagonalvektorer i parallellogram
Parallellogram:
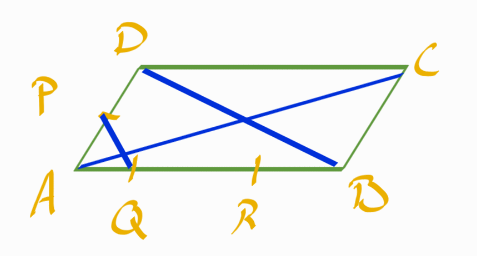
P är mittpunkt på AD. Q och R delar AB i tre lika långa delar.
Jag vill uttrycka vektorn PQ i diagonalvektorerna BD och AC.
Uttrycket blir alltså något i stil med PQ = x BD + y AC, x, y reella.
Känns egentligen som att det är tämligen enkelt (får mig att tänka på ekvationssystem), men fastnar halvvägs:
PQ = PA + AQ
PA = - 1/2 AD
AQ = 1/3 AB
dvs
PQ = -1/2 AD + 1/3 AB.
Därefter är min tanke att byta ut AD och AB mot uttryck innehållande diagonalvektorerna, t ex
AD = AC + CD
AB = AC + CB.
Här börjar jag dock gå i cirklar. Har provat att byta ut t ex AC i ovanstående två ekvationer, eller att uttrycka AD och AB på andra sätt, men hur jag än gör så kommer jag tillbaka där jag startade.
Är detta en rimlig start? Vad saknar jag om jag är på rätt vad?
Kan inte se mönstret i denna typ av problem. Spontana tanken var att jag vill byta ut oönskade vektor tills dess att jag har mitt önskade uttryck.
Jag har inte läst din lösning. Så här tänker jag:
Diagonalerna delar varandra mitt itu. Så
AB = AC/2 + DB/ 2 (jag borde ha pilar)
AQ = AB/3 = AC/6 + DB/6
AD = AC/2 +BD/2
AP = AD/2 = AC/4 + BD/4
PQ = AQ – AP = AC(1/6 – 1/4) + DB/6 — BD/4 = –AC/12 + DB/6 + DB/4 =
= CA/12 + 5 DB /12
Verkar det rätt?
Ja, det är korrekt. Tänkte inte på att diagonalerna delar varandra mitt itu, eller, visste inte man kunde göra så. Då blev det ju enklare. Shysst!
Jag förstår inte i
PQ = AQ – AP = AC(1/6 – 1/4) + DB/6 — BD/4 = –AC/12 + DB/6 + DB/4
= CA/12 + 5 DB /12.
hur AQ blir = AC(1/6 – 1/4), vart kommer 1/4 ifrån?
och hur PA får BD/4?

