Uttryck för potentiell och kinetisk energi

Jag skulle också säga att formeln för potentiell energi gäller just för samma anledning som du angett. Den potentiella energin kommer precis som du nämner från källan som har uträttat ett arbete på föremålet som fått det att "lagra" denna potentiella energi. 

Om man utgår ifrån samma nollnivå för två olika föremål och de lyfts till samma höjd relativt nollnivån så kommer de ha samma potentiell energi (lägesenergi), det finns andra potentiella energier också. Två föremål kan inte ha olika lägesenergi om de har lyfts till samma höjd men de kan ha olika totalenergi, dvs t.ex om man kastar upp en boll i luften så kommer de ha samma lägesenergi vid samma höjd men kanske olika totalenergi eftersom att den ena kanske har en högre hastighet (då har ena bollen en högre rörelseenergi och därmed högre totalenergi).

Ett föremål kommer inte att ha högre lägesenergi eftersom det lyfts upp snabbare eller tvärtom däremot kommer källan som lyft upp föremålet att utvecklat en större effekt, som definieras som arbete utfört dividerat med tiden som det utförts på.

Härledningen för rörelseenergi ur definitionen för arbete är följande, lärde mig faktiskt inte den förrän universitetet så vet inte om det går att härleda den utan att integrera (som i fallet för lägesenergin E=mgh). Under gymnasiet förekommer det ju i princip inga integraler eller derivator i fysiken.

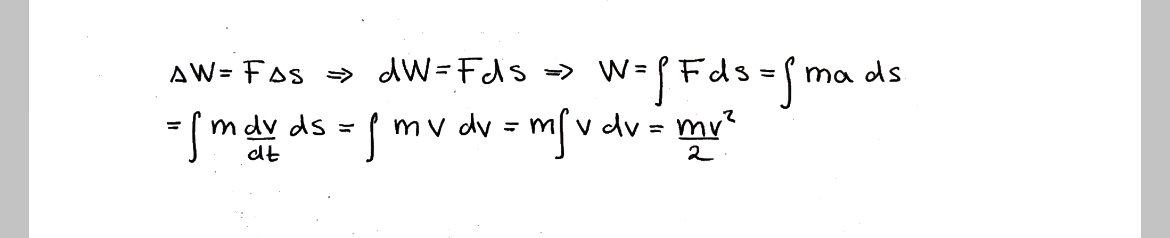
Tack för ditt utförliga svar! 

Vi har inte börjat på integraler ännu så jag är inte helt med på vad som händer men det verkar som om du substituerar $\frac{ds}{dt}$mot $v$. Men hur kan du göra det? Sambandet $s=vt$ gäller väl endast om hastigheten är konstant?

Har ni gått igenom derivator?

Inte egentligen men jag vet vad en derivata är och jag kan vissa av deriveringsreglerna.

Okej, det du säger gällande $s=vt$ stämmer, alltså att sambandet endast gäller vid konstant hastighet.

Men man kan också uttrycka detta på differentialform, alltså $v=\frac{ds}{dt}$.

d:en framför betecknar oändligt små ändringar i varje storhet, detta gör att om vi tar en oändligt liten ändring i dessa storheter i en viss punkt så kan vi se det som att hastigheten är konstant i just den punkten(eftersom ändringen är så liten), vi får då momentanhastigheten, dvs hastigheten i just den tidpunkten. Vi kan observera att detta är just derivatan av en sträcka som en funktion av tiden, eftersom att derivatan berättar för oss vad lutningen på en dragen tangent för funktionen i en given punkt är, (alltså förändringen).

Sedan kan man ta varenda oändligt liten förändring och lägga ihop alla de så att man får en "verklig" förändring, det som betecknas med $∆$, och detta görs genom att integrera.

Förresten, man behöver egentligen inte ens integrera för att komma fram till uttrycket för rörelseenergi. Man kan även använda sig av formeln $v^2-u^2=2a∆s$ (borde stå i formelsamlingen),

där v är sluthastighet och u starthastighet

$∆W=F∆s=ma∆s=m\frac{v^2-u^2}{2∆s}∆s=\frac{m{v}^2}{2}$, om man förutsätter att objektet startar från vila, dvs u=0m/s

Men nu räknar vi väl på hur mycket energi som krävs för att flytta ett stillastående föremål upp i en hastighet (utan friktion)? Eller vilket arbete exakt tittar vi på?

Arbetet som krävs för att få ett föremål att gå från 0 m/s till v m/s, bortsett från energiförluster.