Uppskattar hjälp med tuff integral uppgift
Frågan lyder:
En area begränsas av:
- Funktionen f(x)=k(x-k)2
- x-axeln
- den lodräta linjen genom skärningspunkten mellan f(x)och x-axeln
- linjen x=2
Den roterar kring x-axeln
Vilket ger den maximala volymen om 0<k<2.
Hur jag har tänkt:
Tror att jag är helt ute och cyklar men när jag plottar grafen på grafräknare förstår jag att desto högre k desto större volym så då antar jag att om jag räknar ut integralen och på något sätt får maximum värdet för k kan jag få den största volymen då k är mellan 0 och 2.
efter magi och binomialsatsen
Är nu inte säker hur jag får fram svaret eller om jag helt gör fel då jag kanske måste använda mig av limit för när k --> 2?
Hej och välkommen till Pluggakuten!
Kan du rita och visa en figur som visar området?
Hur tänker du avseende integranden, integrationsgränserna och integrationsriktningen?
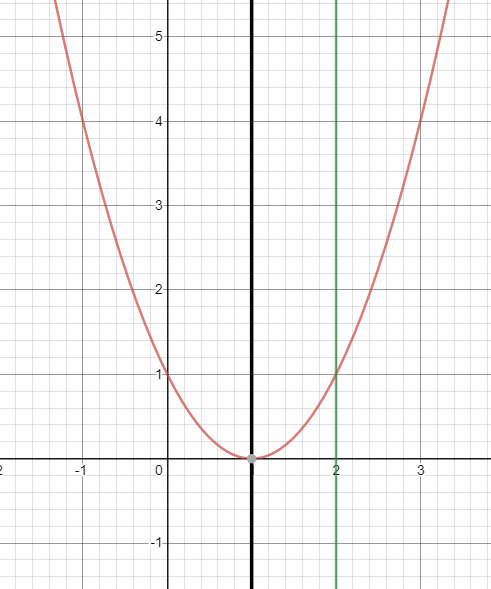
Hej & tack!
Jag läste nog uppgiften lite fel innan med hur jag tänkte grafen skulle vara
Men denna figur visar den röda linjen som är k(x-k)^2 som förflyttar sig sidleds beroende på k.
sedan har den integrationsgränserna 2k(x-k) = 0 och 2 därav
Integranden borde även vara pi*(k(x-k)^2)^2
Vet dock inte vad integrationsriktningen är.
Ja, bra, då ser det rätt ut. Integrationsriktningen är i x-led, från vänster till höger.
Men du behöver varken använda magi eller bonomialsatsen för att bestämma integralens värde.
Det blir ett uttryck som beror av k, dvs volymen V blir en funktion av k. V = V(k).
Det är denna volym du sedan ska försöka maximera.
Förstår tyvärr inte är V(k) = ?
Den undre integrationsgränsen är väl k.
Lös k(x-k)2=0 innan du försöker integrera, så har du integralens undre gräns ;)



