Uppgift 20 i Mafy 2019
jag försökte i c-alternativet men kom inte till något, vad är det för fel jag gör?
Välkommen till Pluggakuten!
Vad handlar uppgiften om? Vad är c-alternativet? Finns det andra alternativ också?
 Tack! Det är den här uppgiften
Tack! Det är den här uppgiften
Att c) även gäller för icke-rätvinklig triangel är ganska besvärligt att visa, så jag föreslår istället att visa att a,b,d medför att triangeln är rätvinklig, varför c) måste vara rätt svar.
Trinity2 skrev:Att c) även gäller för icke-rätvinklig triangel är ganska besvärligt att visa, så jag föreslår istället att visa att a,b,d medför att triangeln är rätvinklig, varför c) måste vara rätt svar.
Kan du förklara mer, vilken a, b,d? Menar du c istället för d
Joumana.math skrev:Trinity2 skrev:Att c) även gäller för icke-rätvinklig triangel är ganska besvärligt att visa, så jag föreslår istället att visa att a,b,d medför att triangeln är rätvinklig, varför c) måste vara rätt svar.
Kan du förklara mer, vilken a, b,d? Menar du c istället för d
a, b och d är enkla att visa att det råder ekvivalens mellan dessa och rätvinklig triangel. Då så är fallet kan dessa 3 förkastas och c är rätt svar. Att visa c är omständigt och lite knepigt.
Trinity2 skrev:Joumana.math skrev:Trinity2 skrev:Att c) även gäller för icke-rätvinklig triangel är ganska besvärligt att visa, så jag föreslår istället att visa att a,b,d medför att triangeln är rätvinklig, varför c) måste vara rätt svar.
Kan du förklara mer, vilken a, b,d? Menar du c istället för d
a, b och d är enkla att visa att det råder ekvivalens mellan dessa och rätvinklig triangel. Då så är fallet kan dessa 3 förkastas och c är rätt svar. Att visa c är omständigt och lite knepigt.
Hur visar jag att d inte stämmer
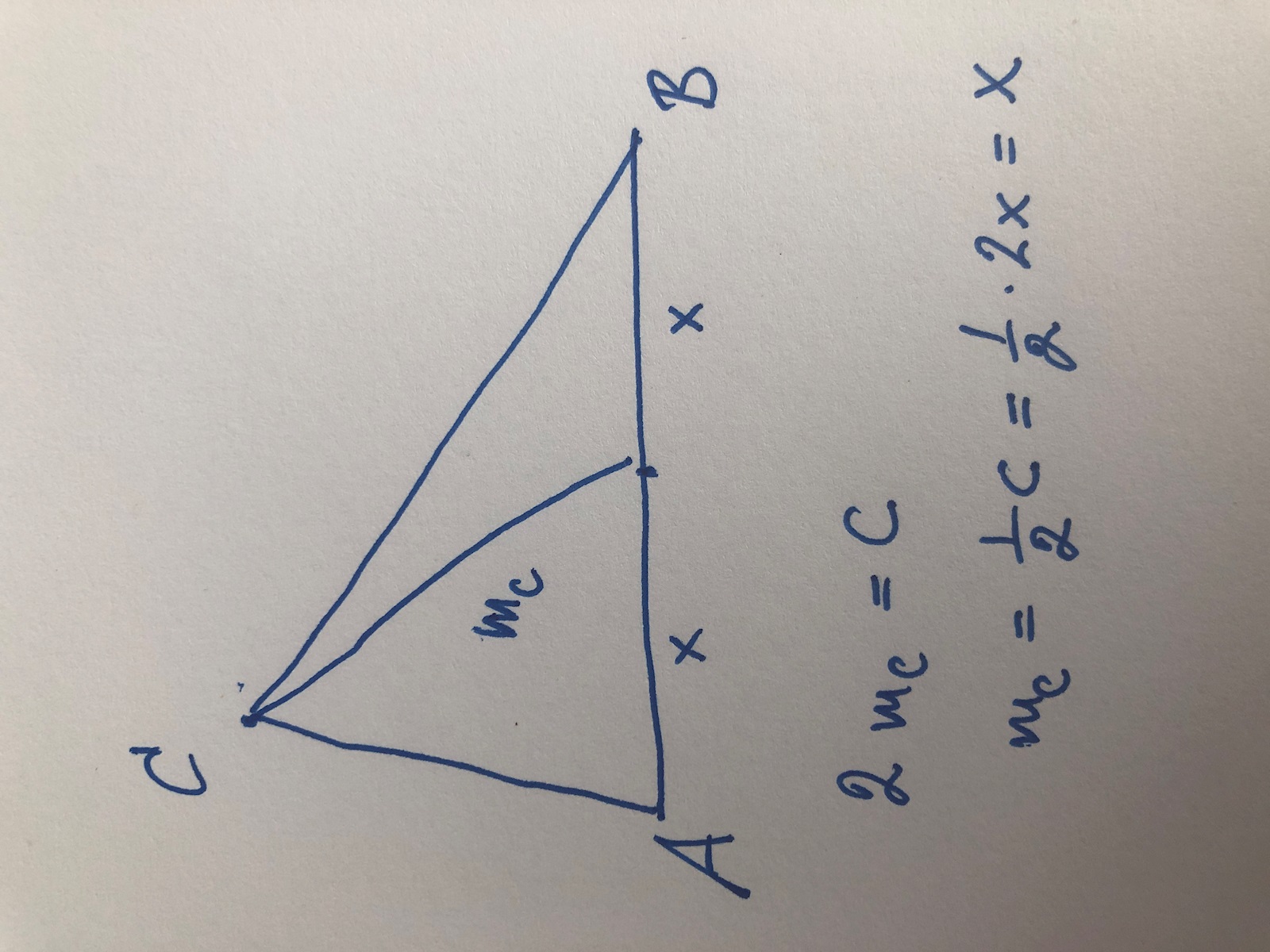
Här ser vi att m_c=x och därmed är x, x, och m_c alla radier i en cirkel med radien x och medelpunkt där medianen träffar AB. AB är alltså en diameter och randvinkelsatsen säger då att vinkeln ACB är 1/2*180°=90°. ABC kan inte vara något annat än rät om 2m_c = c, och omvänt, en rät triangeln uppfyller 2m_c = c.



