Uppgift 2.2 mekanik 2

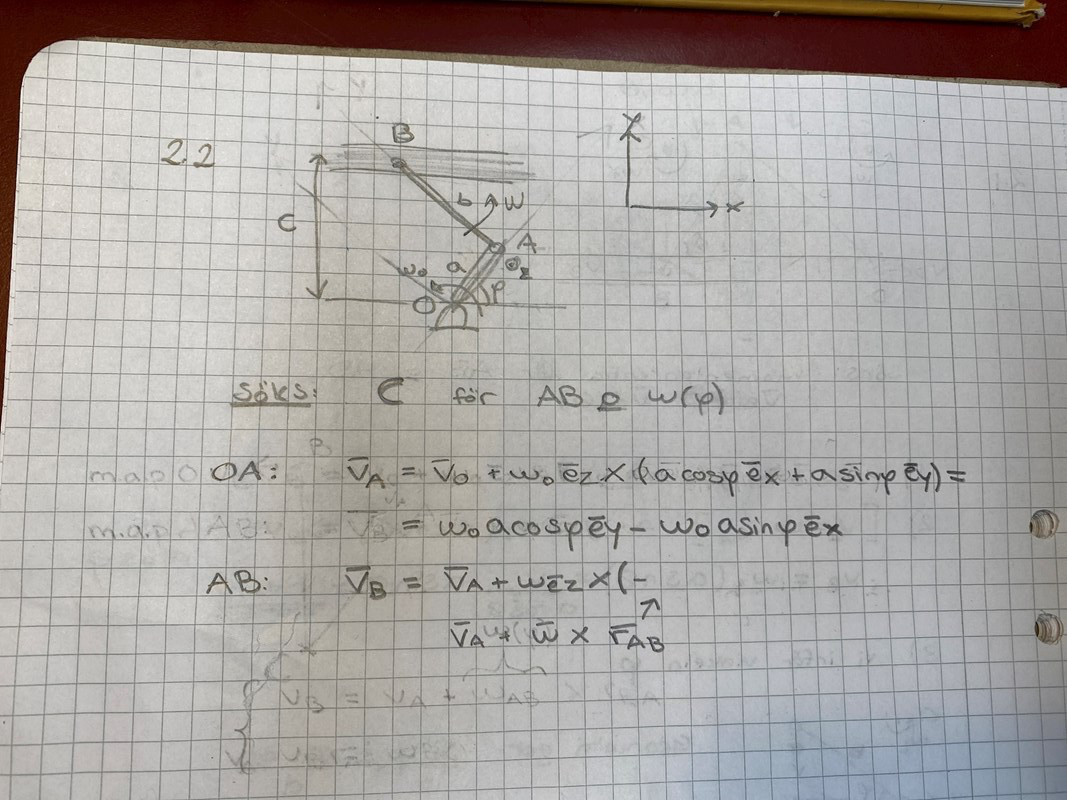 hur ska jag skriva rAB uttryckt i ex och ey?
hur ska jag skriva rAB uttryckt i ex och ey?
Du kan ansätta rB = (xB, c) och sedan utnyttja att |rB - rA| = b.
Det går att hitta momentancentrum med en geometrisk konstruktion.

PATENTERAMERA skrev:Du kan ansätta rB = (xB, c) och sedan utnyttja att |rB - rA| = b.
Det går att hitta momentancentrum med en geometrisk konstruktion.
Tack! Men varifrån kommer rB = (xB, c)?
Origo i O. y-koordinaten är c enligt figur. xB är obekant som bestäms av villkoret att = b.
PATENTERAMERA skrev:Origo i O. y-koordinaten är c enligt figur. xB är obekant som bestäms av villkoret att = b.
Jaha okej!
men hur vet man att C inte hamnar på andra sidan? Dvs vinkelrätt ut fast åt andra hållet

Obs du drar linjer vinkelrät mot hastigheterna och ser var de möts. vB är nog riktad åt andra hållet, men det spelar ingen roll för den vinkelräta linjen blir densamma.
Tillägg: 11 sep 2024 01:17
Du skall alltså dra en linje genom B som är vinkelrät mot vB och en linje genom A som är vinkelrät mot vA. C ligger där linjerna skär varandra.
PATENTERAMERA skrev:Obs du drar linjer vinkelrät mot hastigheterna och ser var de möts. vB är nog riktad åt andra hållet, men det spelar ingen roll för den vinkelräta linjen blir densamma.
Tillägg: 11 sep 2024 01:17
Du skall alltså dra en linje genom B som är vinkelrät mot vB och en linje genom A som är vinkelrät mot vA. C ligger där linjerna skär varandra.
Man drar alltså linjen från hastigheternas startpunkter? För i bilden jag skicka så drog jag linjer från deras verkningslinjer och då kunde jag ju få C på ett annat ställe än du fick?
Du måste dra linjerna genom A och B.


