Uppdrag 2... Matte 3c (Matematik/Matte 3)

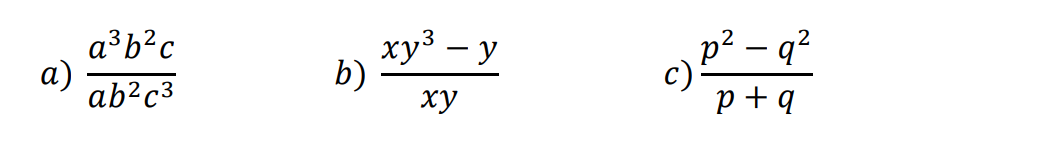
Vad är uppgiften?
Ska uttrycken förenklas så långt det går?

Då gäller det att faktorisera täljare och nämnare och sedan förkorta bråket med gemensam faktorer.

a) Här är de redan faktoriserade. Använd potensreglerna för att förenkla uttrycket.

Arktos skrev:
Vad är uppgiften?
Ska uttrycken förenklas så långt det går?

Då gäller det att faktorisera täljare och nämnare och sedan förkorta bråket med gemensam faktorer.

a) Här är de redan faktoriserade. Använd potensreglerna för att förenkla uttrycket.

ja de ska förenklas.... lyssna jag har inte fått lära mig mycket om potenser och sånt inom grundskolan.. så det är därför jag behöver hjälp...

Tack så mycket!

Arktos skrev:
Vad är uppgiften?
Ska uttrycken förenklas så långt det går?

Då gäller det att faktorisera täljare och nämnare och sedan förkorta bråket med gemensam faktorer.

a) Här är de redan faktoriserade. Använd potensreglerna för att förenkla uttrycket.

Är svaret på A )

a/ c² ? förkortade så långt så möjligt

På B är svaret....)

xy²-y

a³/a =a³/a¹ = a^3-1 = a² (med potenslag).

eller a³/a = a*a*a/a = a*a = a²

Så svaret är a²/c².

I b) börjar du med att bryta ut y i täljaren.
Sedan kan du förkorta bråket med y.
xy² är rätt men inte - y. Och så blir det en nämnare.

Louis skrev:
a³/a =a³/a¹ = a^3-1 = a² (med potenslag).

eller a³/a = a*a*a/a = a*a = a²

Så svaret är a²/c².

I b) börjar du med att bryta ut y i täljaren.
Sedan kan du förkorta bråket med y.
xy² är rätt men inte - y. Och så blir det en nämnare.

Förlåt men förstod inte riktigt... hur löser man det... ifall du kan skriva det som riktigt division lösning,. så borde det vara ännu tydligare... tack!!

Tillägg: 31 aug 2023 17:14

Jag förstod A men inte B.... hur ska jag göra?

Louis skrev:
a³/a =a³/a¹ = a^3-1 = a² (med potenslag).

eller a³/a = a*a*a/a = a*a = a²

Så svaret är a²/c².

I b) börjar du med att bryta ut y i täljaren.
Sedan kan du förkorta bråket med y.
xy² är rätt men inte - y. Och så blir det en nämnare.

Blir det inte på B)....

xy⁽³⁻¹⁾ = xy²

så svaret blir xy² -y ?? eller?

Att du får kvar - y tyder på att du "förkortar" i första termen (termer har plus eller minus mellan sig).
Det kan man inte göra.
Du har t ex att $\frac{5 * 2 + 4}{5} = \frac{14}{5}$ , inte 6 som du får om "stryker" 5:orna.
Också 4:an är ju delad med 5.

$\frac{x y^{3} - y}{x y} = \frac{y (x y^{2} - 1)}{x y} = \frac{x y^{2} - 1}{x}$

Här blev y faktor (gånger) i både täljare och nämnare och kunde förkortas bort.
Sedan kan du inte göra något mer.

Du kan dock skriva $y^{2} - \frac{1}{x}$ .

Vart tog ditt x i nämnaren vägen?

Louis skrev:
Att du får kvar - y tyder på att du "förkortar" i första termen (termer har plus eller minus mellan sig).
Det kan man inte göra.
Du har t ex att $\frac{5 * 2 + 4}{5} = \frac{14}{5}$ , inte 6 som du får om "stryker" 5:orna.
Också 4:an är ju delad med 5.

$\frac{x y^{3} - y}{x y} = \frac{y (x y^{2} - 1)}{x y} = \frac{x y^{2} - 1}{x}$

Här blev y faktor (gånger) i både täljare och nämnare och kunde förkortas bort.
Sedan kan du inte göra något mer.

Du kan dock skriva $y^{2} - \frac{1}{x}$ .

Vart tog ditt x i nämnaren vägen?

x tog vägen med..... 1/x.... eller?

Jag menade när du fick xy² - y och nämnaren x försvann.

Louis skrev:
Jag menade när du fick xy² - y och nämnaren x försvann.

ahaaa... jag gjorde som första uppgiften a)

Potenslagar.....xy³ ⁻¹ för det finns en xy i täljaren...eller är det fel?

Nämnaren är xy och du har xy som faktor i täljarens första term.
Men som jag skrev förut kan du inte förkorta i termer.
Jag var nyfiken på hur du tänkte, eftersom x försvann i nämnaren men var kvar i täljaren.
Tänkte du att jag har xy³, förkortar med xy, då blir det xy² kvar?

Men xy³ betyder x*y*y*y (3:an är bara exponent till y) och om du kan förkorta med xy (som du inte kan här) blir det y² kvar.

Se min lösning i #8. Du måste först faktorisera täljaren och kan bara förkorta bort faktorer som är lika i täljaren och nämnaren.

Louis skrev:
Nämnaren är xy och du har xy som faktor i täljarens första term.
Men som jag skrev förut kan du inte förkorta i termer.
Jag var nyfiken på hur du tänkte, eftersom x försvann i nämnaren men var kvar i täljaren.
Tänkte du att jag har xy³, förkortar med xy, då blir det xy² kvar?

Men xy³ betyder x*y*y*y (3:an är bara exponent till y) och om du kan förkorta med xy (som du inte kan här) blir det y² kvar.

Se min lösning i #8. Du måste först faktorisera täljaren och kan bara förkorta bort faktorer som är lika i täljaren och nämnaren.

ahaaa... jag tänkte att hela xy tas tre gånger.....

så det är därför jag gjorde xy³ - xy så det är xy² kvar...

nu förstår jag din lösning....

men hur ska jag skriva det som slutlig lösning steg för steg?

Det jag skrev i #8 är hela lösningen: bryt ut y i täljaren, förkorta med y.
I den här uppgiften gick det inte att förenkla mer.
I både a) och c) kunde man förenkla mer (så att det inte blev så mycket kvar).

Louis skrev:
Det jag skrev i #8 är hela lösningen: bryt ut y i täljaren, förkorta med y.
I den här uppgiften gick det inte att förenkla mer.
I både a) och c) kunde man förenkla mer (så att det inte blev så mycket kvar).

så är detta rätt?

xy³-y / xy = x*y*y*y-y/x*y = y*y-y = y²-y

eller??

för jag förkortade med y på nämnaren och täljaren.... samma med x på såda sidorna. för det finns x i både leden så jag förkortade de oxå.... rätt eller?

Inlägget redigerat, eftersom jag nu tycker mig se vad du gör.

Om du jämför med lösningen i #8 ser du att det inte är rätt.

Det ser fortfarande ut som att du förkortar i termer.
I #8 visade jag ett exempel med bara tal varför man inte kan "stryka" en faktor inne i en term i täljaren mot en faktor i nämnaren, 5 i det exemplet.

Kan du "läsa av" ett uttryck med avseende på termer (plus och minus) och faktorer (gånger)?
Alltså se hur det är uppbyggt. I uppgift b) består täljaren av två termer.
Första termen xy³ består av två eller fyra faktorer, beroende på om vi räknar y³ som en eller tre faktorer (y*y*y).
Nämnaren består av två faktorer, x och y.
Det här är viktigt, för att du ska se vad du kan göra med ett uttryck.
Du kan alltså inte "stryka" faktorn xy i nämnaren (hela nämnaren kan också uppfattas som en faktor) mot xy i täljarens första term. Båda termerna i täljaren är ju delade med nämnarens xy. Du måste först faktorisera täljaren, och det kan du göra genom att bryta ut y (se #8). x-faktorerna kan du inte göra något med i den här uppgiften.
Är du med på de här resonemangen?

Eller om vi tar ett sådant här exempel där du genast ser svaret:
3 personer ska dela på 3 äpplen och 6 päron. Vad får var och en?
Då skulle du inte säga (3 äpplen + 6 päron)/3, det är en 3:a både uppe och nere, då kan jag stryka dem så att svaret blir 1 äpple och 6 päron till var och en.
Däremot kan du bryta ut 3 i täljaren så att du får 3(1 äpple + 2 päron)/3.
Då 3 är en faktor både i täljare och nämnare kan du "stryka" dem, dvs förkorta med 3
(dela täljare och nämnare med 3), så att svaret blir det du visste från början:
1 äpple + 2 päron till var och en.
Det är samma sak i uppgift b), alltså varför du inte kan "stryka" nämnarens xy mot xy i täljarens första term.

Om du använder / som divisionstecken/bråkstreck behöver du använda parenteser: (xy³-y)/xy.
Det du skriver betyder xy³ - $\frac{y}{x y}$ och det är något annat.

Louis skrev:
Inlägget redigerat, eftersom jag nu tycker mig se vad du gör.

Om du jämför med lösningen i #8 ser du att det inte är rätt.

Det ser fortfarande ut som att du förkortar i termer.
I #8 visade jag ett exempel med bara tal varför man inte kan "stryka" en faktor inne i en term i täljaren mot en faktor i nämnaren, 5 i det exemplet.

Kan du "läsa av" ett uttryck med avseende på termer (plus och minus) och faktorer (gånger)?
Alltså se hur det är uppbyggt. I uppgift b) består täljaren av två termer.
Första termen xy³ består av två eller fyra faktorer, beroende på om vi räknar y³ som en eller tre faktorer (y*y*y).
Nämnaren består av två faktorer, x och y.
Det här är viktigt, för att du ska se vad du kan göra med ett uttryck.
Du kan alltså inte "stryka" faktorn xy i nämnaren (hela nämnaren kan också uppfattas som en faktor) mot xy i täljarens första term. Båda termerna i täljaren är ju delade med nämnarens xy. Du måste först faktorisera täljaren, och det kan du göra genom att bryta ut y (se #8). x-faktorerna kan du inte göra något med i den här uppgiften.
Är du med på de här resonemangen?

Eller om vi tar ett sådant här exempel där du genast ser svaret:
3 personer ska dela på 3 äpplen och 6 päron. Vad får var och en?
Då skulle du inte säga (3 äpplen + 6 päron)/3, det är en 3:a både uppe och nere, då kan jag stryka dem så att svaret blir 1 äpple och 6 päron till var och en.
Däremot kan du bryta ut 3 i täljaren så att du får 3(1 äpple + 2 päron)/3.
Då 3 är en faktor både i täljare och nämnare kan du "stryka" dem, dvs förkorta med 3
(dela täljare och nämnare med 3), så att svaret blir det du visste från början:
1 äpple + 2 päron till var och en.
Det är samma sak i uppgift b), alltså varför du inte kan "stryka" nämnarens xy mot xy i täljarens första term.

Om du använder / som divisionstecken/bråkstreck behöver du använda parenteser: (xy³-y)/xy.
Det du skriver betyder xy³ - $\frac{y}{x y}$ och det är något annat.

Tack för all hjälp!!