Undre integrationsgräns
Hej!
Frågan är: Beräkna arean av det ändliga område som begränsas av kurvan y=tan(x) , x-axeln samt linjen x=.
Det står inte "som begränsas av positiva x-axeln" så är lite förvirrad hur jag avgöra undre integrationsgränsen.
I facit står det: Integrationsgränser ges av ekvationen tan(x)=0 <--> x=0+n. Enkel skiss ger vid handen att vi får undre integrationsgräns x=0.
Jag tror jag förstår men är inte helt säker.
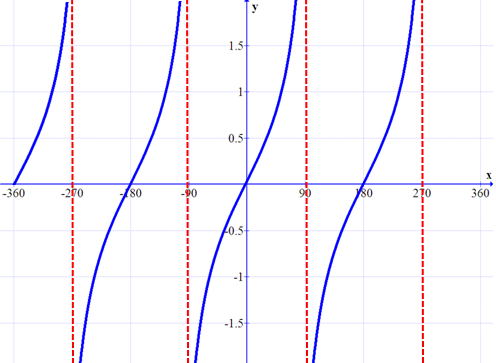
Liksom graf till tanx har kurvade lodräta linjer som är växande med gränsvärden vid början och slutet av varje period. x=pi/4 är en rät linje som går lorätt. Ger det att vi får intervallet -90<x<90, iom att det är enda kurvan som begränsas av x=pi/4, där enda vinkeln i givna intervall är x=0?
Hoppas det här var begripligt.. Svårt att utrycka sig i text när det kommer till matte.
Bumpar tråden
Eftersom det står y= tan(x), x-axeln och x = pi/4 och att funktionen tan(x) går igenom origo tycker jag att det är klart att det ska integreras mellan 0 och pi/4
Okej, tack då är jag med!