Undersök om matris-följden A^n konvergerar, och i så fall mot vilken matris? (Mathematica)
Hej!
Jag har tittat på liknande inlägg här på pluggakuten men blir inte något klokare. Vi ska arbeta i programmet Mathematica och använda oss av dess olika funktioner för att lösa problem.
Uppgiften är:
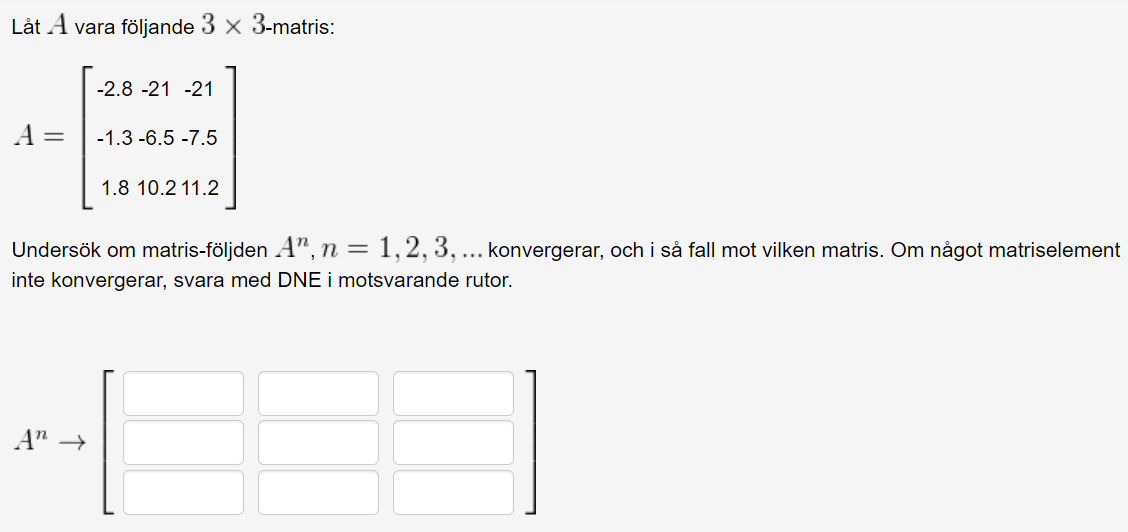
Det första jag har gjort är att skriva in raderna för matrisen i Mathematica med {} och sedan MatrixForm[A]. Så långt går det bra.
Sedan har jag läst lite på Mathematicas egna hjälpsidor men fattar ingenting, i något tidigare inlägg här skriver folk om MatrixPower[] och jag förstår inte riktigt hur jag ska använda det.
Hur börjar jag?
Jag förstår inte heller på vilket sätt den ska konvergera, vad ska konvergera?
Prova att räkna ut A10 och A20.
Laguna skrev:Prova att räkna ut A10 och A20.
Tänker du att jag ska multiplicera A med A10 och A20 för att testa om den konvergerar då?
Är det så du menar?
Om du multiplicerar A med A10 får du A11. Börja med A10.
I Mathematica använder du MatrixPower[m,n] för att beräkna matrispotenser
Om du kallar din matris A kan du alltså skriva (för att räkna ut
MatrixPower[A,10] D4NIEL skrev:I Mathematica använder du MatrixPower[m,n] för att beräkna matrispotenser
Om du kallar din matris A kan du alltså skriva (för att räkna ut
MatrixPower[A,10]
Så det jag ska göra är att testa mig fram genom att först mata in matris A och sedan testa att istället för n i formeln sätta in t.ex. 10, 20 eller annat för att se om jag "kommer tillbaka" till A:s matris?
Jag ursäktar om jag ställer dumma frågor.
Ja, men det är inte säkert att du kommer tillbaka till A. Däremot borde det vara så att A10 är ganska lik A20 på många ställen.
Laguna skrev:Ja, men det är inte säkert att du kommer tillbaka till A. Däremot borde det vara så att A10 är ganska lik A20 på många ställen.
Men vad menas med att jag ska ta reda på var matrisen konvergerar, jag förstår inte begreppet "kovergera".
Det jag kan se är att sista två raderna i matrisen blir c:a {-1,-4,-5} och {1,4,5} både för A20, A30, A40 etc. Medan första raden i matrisen blir mer och mer olik för varje exponenthöjning.
Är det detta som är svaret? För jag får inte rätt på uppgiften.
Den första raden går förmodligen mot noll, hur stora tal får du och minskar de ju mer du ökar ?
Nu kom jag på det!
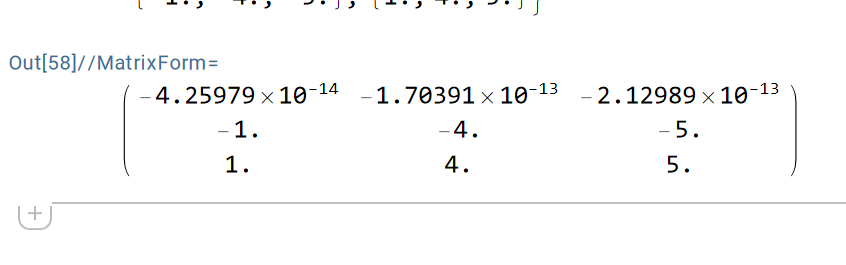
A200 och A400 blir helt lika varandra!
Då blev matrisen som ovan!
Tack för all hjälp!
Tanken är att du ska se att den övre raden blir mindre och mindre. Slutligen kommer datorns oförmåga att hantera små tal göra att det inte blir så stor skillnad mellan ökande . Maskinprecisionen räcker helt enkelt inte till.
Men alla element i första raden konvergerar mot 0.


