undersök om f har en minimipunkt
hej! jag skulle vilja få en ledtråd hur man ska tänka här på fråga b, har läst på att det handlar om gränsvärdet men det förstår jag inte. skulle vara tack för en förklaring :)
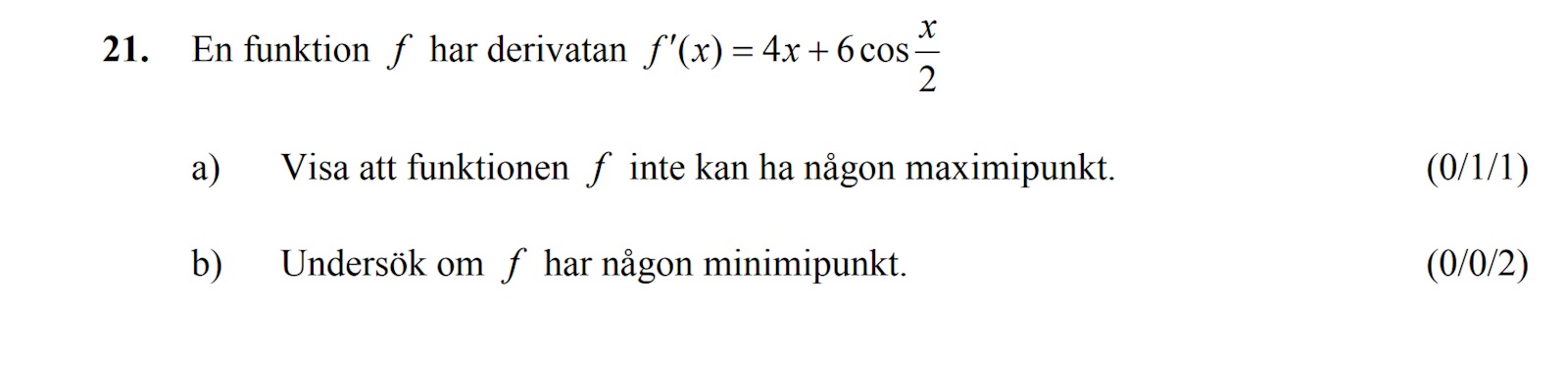
Andra derivatan kanske?
f’(x) = 0 är ekvivalent med x = –(3/2)cos(x/2)
Högerledet pendlar mellan –1,5 och +1,5.
Så vi behöver inte bekymra oss om |x| > 1,5, där kan det inte finnas nollställen.
1,5 är litet mindre än pi/2 så vi kan titta på –1,5cos(x/2) i intervallet
–pi/2 < x < pi/2.
x. –pi/2 0. pi/2
–1,5cos(x/2). ≈ –1. –1,5. ≈ –1
x–1,5cos(x/2). Negativt. Negativt. Positivt
Någonstans mellan 0 och pi/2 är f’(x) = 0. Det är enda nollstället.
(Ska man vara petig behöver man kanske visa det, men det är tämligen uppenbart.)
f(x) avtar till vänster och växer till höger om derivatans nollställe. Så där har f(x) ett minimum. Men ytterligare nollställen finns inte så maximipunkter saknas.
Jo, vid närmare eftertanke håller jag med. Andraderivatan är alltid positiv, därför finns inget maximum. Förstaderivatan är noll på ett ställe, där måste vi ha minimum.
är det svaret på b?
Jag tänkte att det vore svaret på både a och b.
A) Att andraderivatan alltid är positiv visar att det inte kan finnas maximum.
B) Att derivatan är lika med 0 i en punkt visar att det finns minimum.
Att derivatan bara har ett nollställe (vet inte om det måste visas, det känns självklart) visar att det inte kan finnas något mer minimum.


