Underrum och linjära kombinationer.
Har fått en uppgift som komplettering för kursen linjär algebra och jag har ingen aning om hur jag ska göra över huvud taget.  Jag hör löst A vilket säger att du kan skapa u1 utav 3u2+4u3.
Jag hör löst A vilket säger att du kan skapa u1 utav 3u2+4u3.
Men jag vet inte riktigt hur jag ska göra på b. Som jag tyder uppgiften så måste jag använda linjära kombinationer av alla 4 vektorerna för att hitta basen U. Men när jag söker omkring delar alla upp det i mindre ''span'' på oftast 2-3 vektorer. Är det någon som kan ge mig en hint på hur jag ska tänka eller länka en bra video som kan hjälpa till?
Om jag gör sätter vektorerna = 0 och gör gauss elemination så kommer jag fram till att U1, U2 och U4 kommer span underrummet R^3. Är det mitt svar?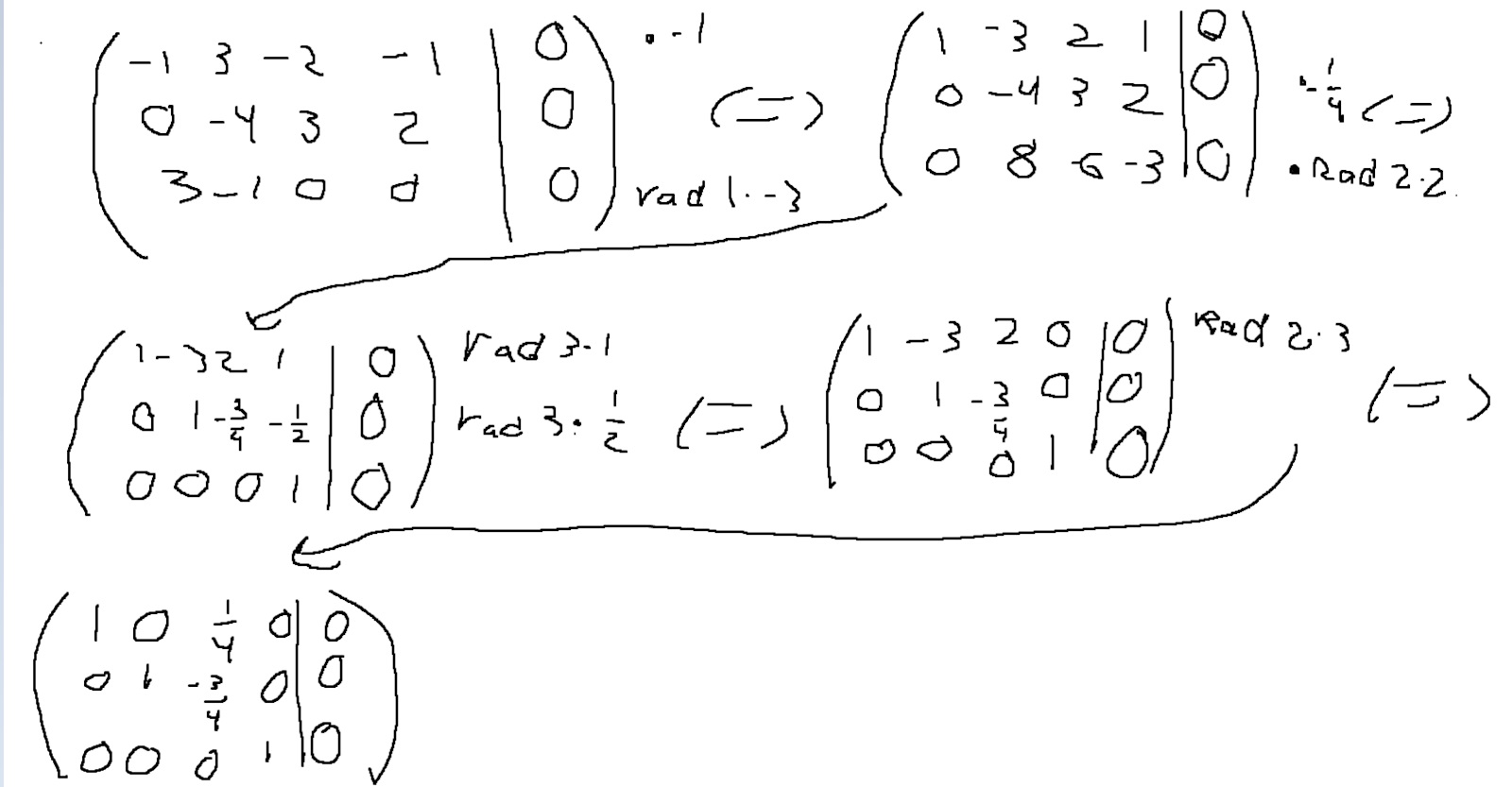
a)-uppgiften kan man egentligen lösa direkt genom att säga att om vi rör oss i R3 så kan vi som mest få tre (3) stycken linjärt oberoende vektorer, och eftersom vi har fyra så måste åtminstone en av dem kunna skrivas som en linjärkombination av de andra.
Ett förstasteg på b)-uppgiften är bilda en matris som innehåller tre av vektorerna och kontrollera determinanten. Om den är nollskild vet vi om att vektorerna är linjärt oberoende och därmed spänner upp hela R3. Nackdelen är bara den att om du skulle råka få med u1, u2 och u3 så skulle du få determinanten 0, men i det läget vet du att en av vektorerna vilken som helst av u1, u2 och u3 är överflödig och kan bilda en ny matris där en av dem ersatts med u4. Får du fortfarande determinanten 0 så vet du att hela rummet R3 inte spänns upp.
Bedinsis skrev:a)-uppgiften kan man egentligen lösa direkt genom att säga att om vi rör oss i R3 så kan vi som mest få tre (3) stycken linjärt oberoende vektorer, och eftersom vi har fyra så måste åtminstone en av dem kunna skrivas som en linjärkombination av de andra.
Ett förstasteg på b)-uppgiften är bilda en matris som innehåller tre av vektorerna och kontrollera determinanten. Om den är nollskild vet vi om att vektorerna är linjärt oberoende och därmed spänner upp hela R3. Nackdelen är bara den att om du skulle råka få med u1, u2 och u3 så skulle du få determinanten 0, men i det läget vet du att en av vektorerna vilken som helst av u1, u2 och u3 är överflödig och kan bilda en ny matris där en av dem ersatts med u4. Får du fortfarande determinanten 0 så vet du att hela rummet R3 inte spänns upp.
Så jag ska alltså bilda 3x3 matriser och testa mig fram tills determinanten inte är 0?
Göra u1 u2 u3, u2 u3 u4 osv tills jag får någon skilt från 0.
Om jag får ett svar skilt från 0 innebär det att jag inte behöver testa resterande kombinationer?
Nej, i det här fallet behöver du bara testa två determinanter.
Gör du på en u1,u2,u3-matris kommer du få determinanten 0. Detta innebär att u1 kan beskrivas som en linjärkombination av u2 och u3 och att u2 kan beskrivas som en linjärkombination av u3 och u1 och att u3 kan beskrivas som en linjärkombination av u1 och u2. Eller det finns förstås möjligheten att två av vektorerna är identiska så när som på en skalfaktor men om man tittar på vektorerna inser man snabbt att så inte är fallet.
Därför så vet du att de vektorer man kan bilda mha. u1,u2,u3 är exakt desamma som de man kan bilda med bara u1,u2.
Sedan tar du determinanten på u1,u2,u4. Skulle denna matris vara 0 skulle det innebära att u1 kan beskrivas som en linjärkombination av u2 och u4 och att u2 kan beskrivas som en linjärkombination av u4 och u1 och att u3 kan beskrivas som en linjärkombination av u1 och u4. Därmed vet du om att hela R3 inte spänns upp, och inga fler determinanter behövs räknas ut.
Om du däremot får en nollskild determinant så vet du att de tre vektorerna i aktuell matris spänner upp hela rummet, och ytterligare test är onödiga.
Jag känner mig en smula ringrostig vad gäller detta, men då jag tittar på inlägg #2 tycker jag att du använder rätt metod men på lite felaktigt vis. Du vill bevisa att man för att bilda nollvektorn som en linjärkombination av våra vektorer måste man multiplicera alla vektorer med 0. Alternativt ta reda på vilka värden man kan multiplicera med våra vektorer för att få nollvektorn, oavsett vilket, mha. Gaussning. Jag tror dock det blir lite fel om man har med alla fyra vektorerna eftersom att vi då kommer hitta att man kan multiplicera u4 med 0 och sedan ta u1, u2 och u3 så att de för sig tar ut varandra(dessa var ju, som du kom fram till, linjärt beroende).
Bedinsis skrev:Nej, i det här fallet behöver du bara testa två determinanter.
Gör du på en u1,u2,u3-matris kommer du få determinanten 0. Detta innebär att u1 kan beskrivas som en linjärkombination av u2 och u3 och att u2 kan beskrivas som en linjärkombination av u3 och u1 och att u3 kan beskrivas som en linjärkombination av u1 och u2. Eller det finns förstås möjligheten att två av vektorerna är identiska så när som på en skalfaktor men om man tittar på vektorerna inser man snabbt att så inte är fallet.
Därför så vet du att de vektorer man kan bilda mha. u1,u2,u3 är exakt desamma som de man kan bilda med bara u1,u2.
Sedan tar du determinanten på u1,u2,u4. Skulle denna matris vara 0 skulle det innebära att u1 kan beskrivas som en linjärkombination av u2 och u4 och att u2 kan beskrivas som en linjärkombination av u4 och u1 och att u3 kan beskrivas som en linjärkombination av u1 och u4. Därmed vet du om att hela R3 inte spänns upp, och inga fler determinanter behövs räknas ut.
Om du däremot får en nollskild determinant så vet du att de tre vektorerna i aktuell matris spänner upp hela rummet, och ytterligare test är onödiga.
Jag känner mig en smula ringrostig vad gäller detta, men då jag tittar på inlägg #2 tycker jag att du använder rätt metod men på lite felaktigt vis. Du vill bevisa att man för att bilda nollvektorn som en linjärkombination av våra vektorer måste man multiplicera alla vektorer med 0. Alternativt ta reda på vilka värden man kan multiplicera med våra vektorer för att få nollvektorn, oavsett vilket, mha. Gaussning. Jag tror dock det blir lite fel om man har med alla fyra vektorerna eftersom att vi då kommer hitta att man kan multiplicera u4 med 0 och sedan ta u1, u2 och u3 så att de för sig tar ut varandra(dessa var ju, som du kom fram till, linjärt beroende).
Om jag då räknat rätt får jag att determinanten av u1, u2 och u4 blir -4. Är mitt svar då att basen U = u1 ,u2 ,u4 eller vad är det jag svarar med? Har inte riktigt förstått den lilla detaljen vad en bas ÄR. Men om jag fattat rätt är det några vektorer som utgör en bas.
Som sagt är jag ringrostig, så om vi tar ett exempel där vektorerna endast spänner upp ett underrum:
v1= (2,0,0)
v2= (0,4,0)
v3= (1,1,0)
Här kan vi aldrig röra oss i den tredje koordinaten, så det underrum som spänns upp av ovanstående vektorer skulle man kunna säga är (x,y,0), x,y € R.
Några vektorer som utgör en bas i detta underrum (ej normerad eller någonting) är ju t.ex. v1 och v2, ty man når hela underrummet mha. dessa vektorerna i linjärkombination.
Så jag skulle säga att u1, u2 och u4 tillsammans utgör en bas till rummet.
Du behöver nog läsa på lite om vad en bas är.
Vidare har du redan mha Gausseliminationen kommit fram till:

(förutom att du missade ett minustecken framför . Eftersom elementära radoperationer bevarar förhållandet mellan kolonnerna säger kolonn tre i din elimination att
Alltså kan man utan att bemöda sig ytterligare välja som bas för underrummet. Du har "rensat höljet"
Det går naturligtvis att välja ett oändligt antal andra baser också, men när du redan gjort en så fin och nästan korrekt elimination kan man ju lika gärna använda den...
D4NIEL skrev:Du behöver nog läsa på lite om vad en bas är.
Vidare har du redan mha Gausseliminationen kommit fram till:
(förutom att du missade ett minustecken framför . Eftersom elementära radoperationer behåller förhållandet mellan kolonnerna säger kolonn tre i din elimination att
Alltså kan man utan att bemöda sig ytterligare välja som bas för underrummet. Du har "rensat höljet"
Det går naturligtvis att välja ett oändligt antal andra baser också, men när du redan gjort en så fin och nästan korrekt elimination kan man ju lika gärna använda den...
Men då får jag tacka er båda. Och så lämnar jag in uppgiften med svaret u1, u2 och u4. Tack för hjälpen!

