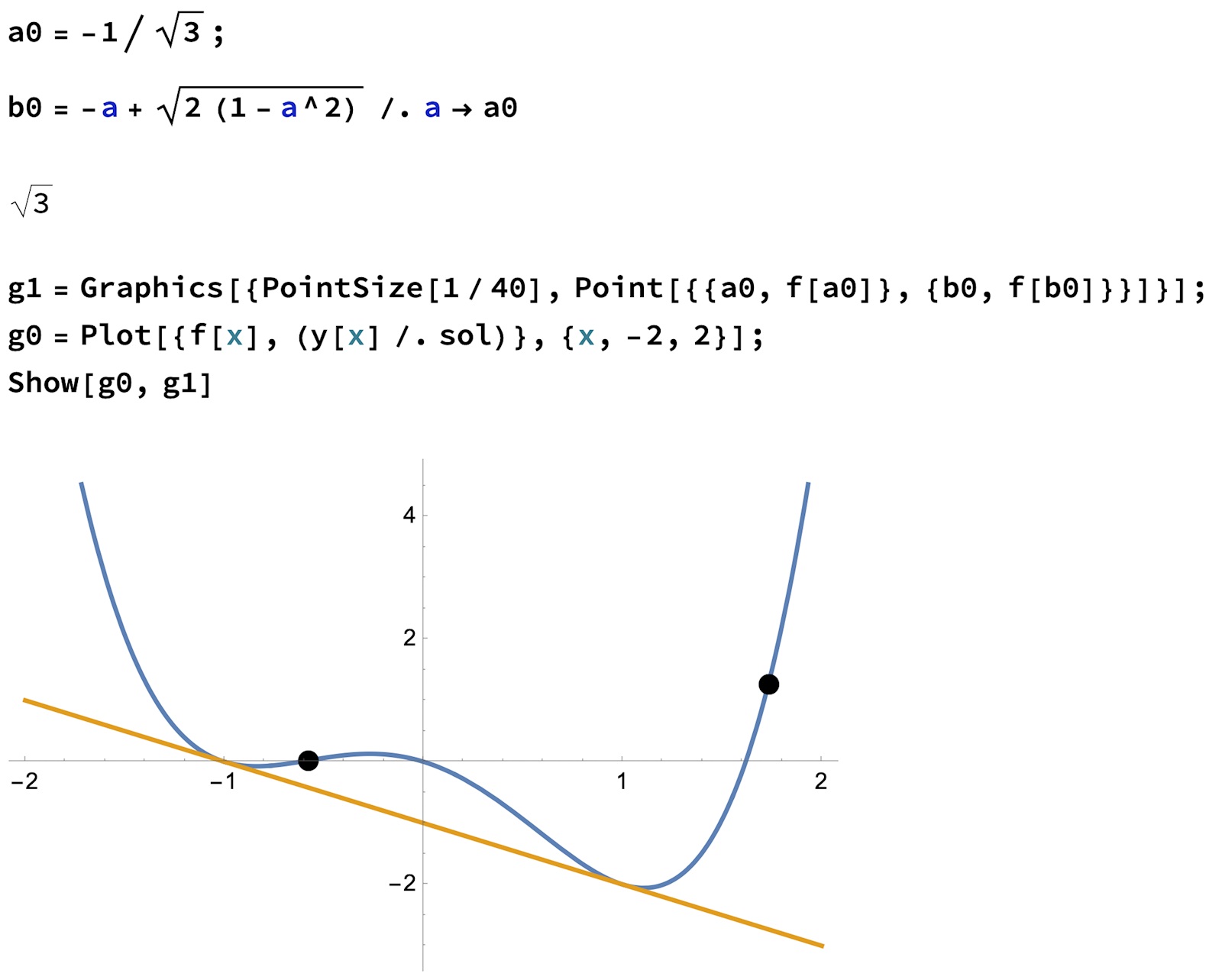
Två punkter på kurva har samma tangentlinje
Hur ska jag börja med denna uppgiften? Har skrivit in funktionen på geogebra men kommer ingen vart
tack på förhand!

Börja med en lättare variant, t.ex. att hitta tangenten där x=1.
Kan du få fram den? Då har du en fungerande metod för att ta fram fler tangenter.
Bubo skrev:Börja med en lättare variant, t.ex. att hitta tangenten där x=1.
Kan du få fram den? Då har du en fungerande metod för att ta fram fler tangenter.
Om jag gör det för hand tar jag derivaran av funktionen, stoppar in det aktuelle x-värdet och sedan använder jag mig av en annan punkt för att få ut m-värdet. Finns det något sätt att göra så att geogebra gör detta åt mig?
Jag skulle rita kurvan först för att förstå uppgiften bättre.
Laguna skrev:Jag skulle rita kurvan först för att förstå uppgiften bättre.
Japp, det tänkte jag med så det har jag gjort
Edit: Tänkte fel.
Intressant uppgift. Har verkligen TS löst den? Inte trivial.
Trinity2 skrev:Intressant uppgift. Har verkligen TS löst den? Inte trivial.
Ja intressant är den, min mattelärare gillar att ge oss sådana provfrågor. Jag lyckades få fram ett svar, men jag räknade inte fram den algebraiskt utan provade mig fram i geogebra och bevisade det sedan algebraiskt. Så egentligen räknas det inte, men min lärare godkände det. Hade varit intressant att höra om det finns andra idéer på hur man kan räkna fram den :)
amyc skrev:Trinity2 skrev:Intressant uppgift. Har verkligen TS löst den? Inte trivial.
Ja intressant är den, min mattelärare gillar att ge oss sådana provfrågor. Jag lyckades få fram ett svar, men jag räknade inte fram den algebraiskt utan provade mig fram i geogebra och bevisade det sedan algebraiskt. Så egentligen räknas det inte, men min lärare godkände det. Hade varit intressant att höra om det finns andra idéer på hur man kan räkna fram den :)
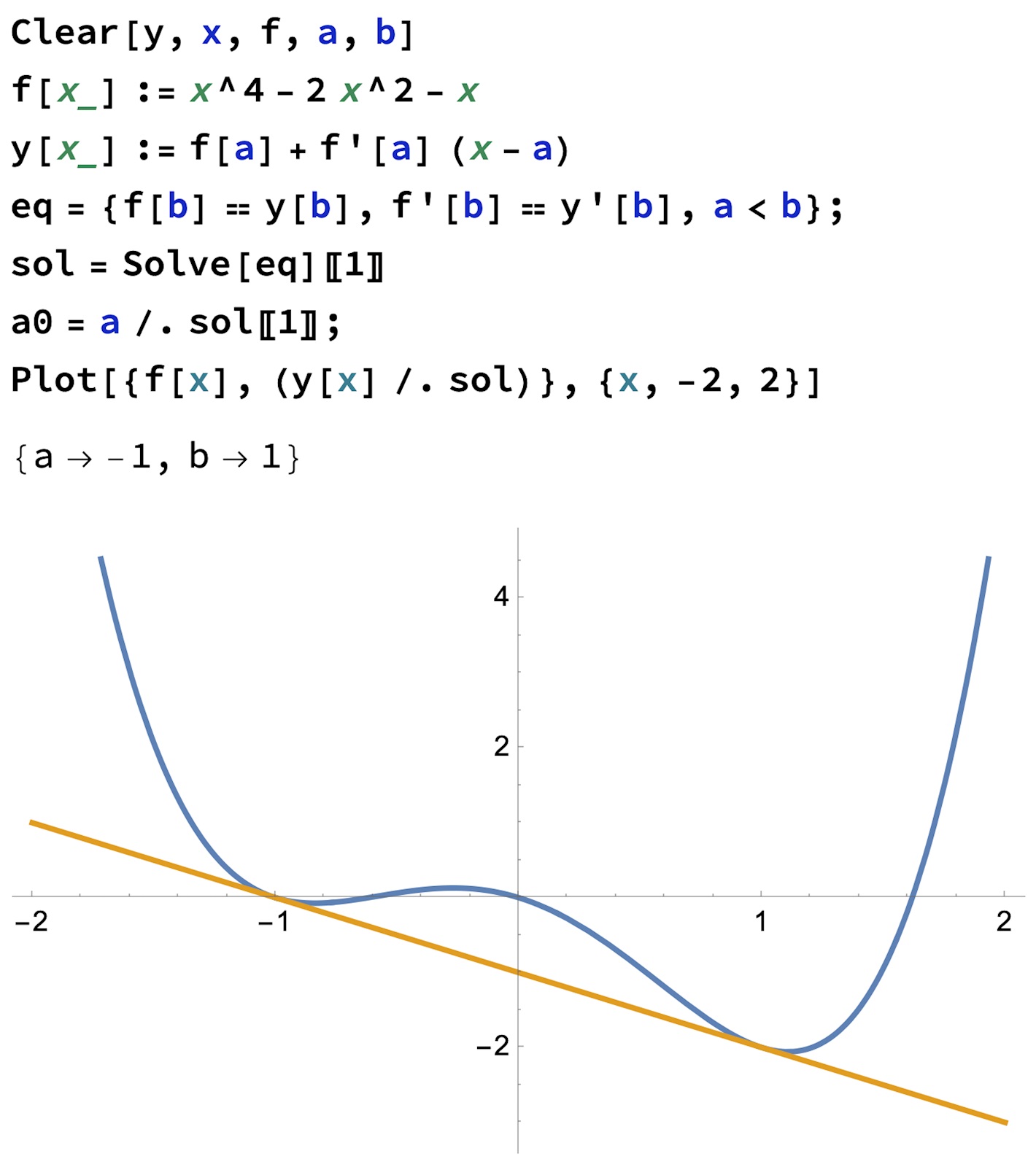
Om vi bortser från manuell räkning, som jag inte gjort (ännu) så skriver man så här i Mathematica
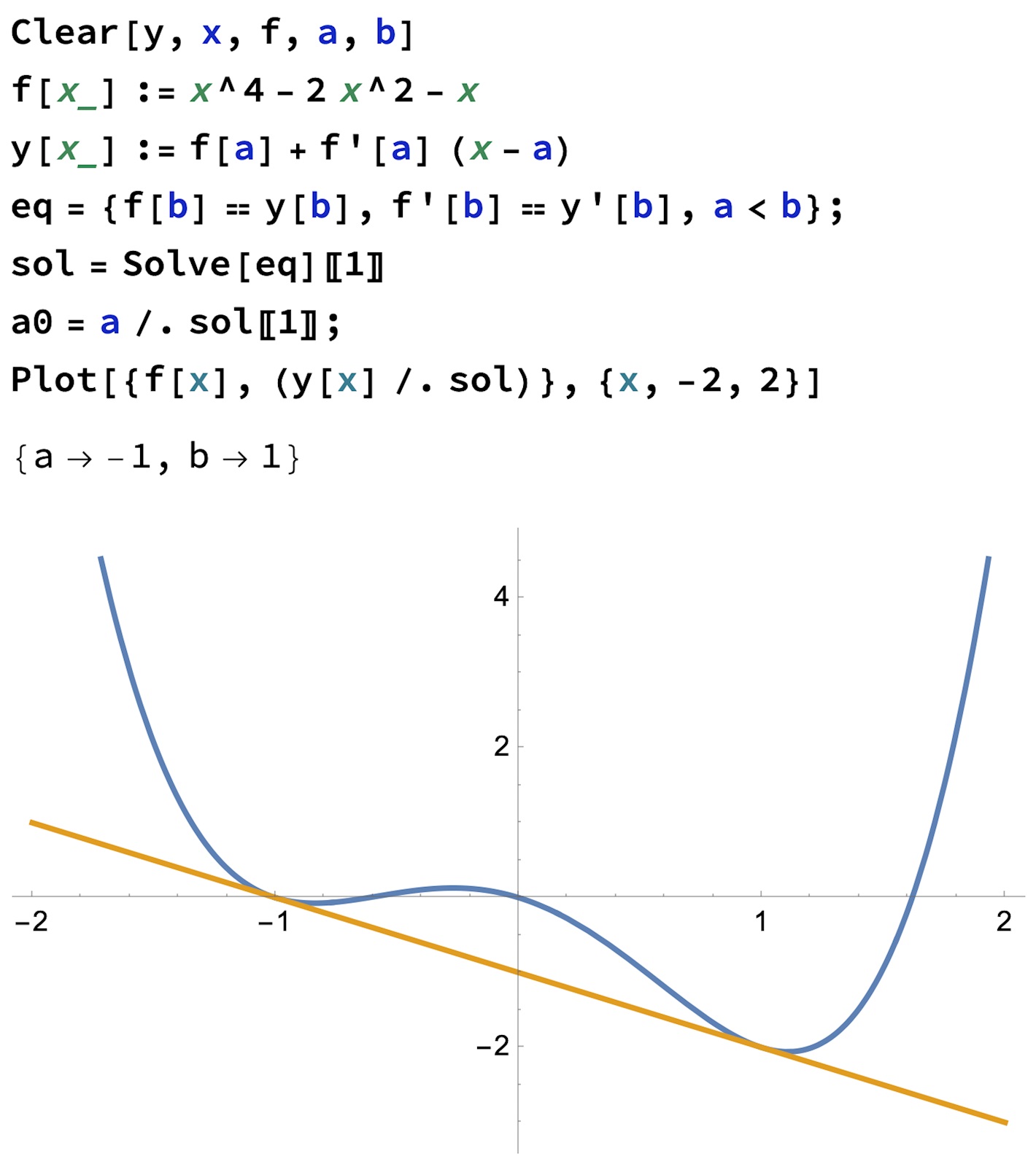
a0-raden behövs ej.
Trinity2 skrev:amyc skrev:Trinity2 skrev:Intressant uppgift. Har verkligen TS löst den? Inte trivial.
Ja intressant är den, min mattelärare gillar att ge oss sådana provfrågor. Jag lyckades få fram ett svar, men jag räknade inte fram den algebraiskt utan provade mig fram i geogebra och bevisade det sedan algebraiskt. Så egentligen räknas det inte, men min lärare godkände det. Hade varit intressant att höra om det finns andra idéer på hur man kan räkna fram den :)
Om vi bortser från manuell räkning, som jag inte gjort (ännu) så skriver man så här i Mathematica
a0-raden behövs ej.
Ahaa, okej tack så mycket!
amyc skrev:Bubo skrev:Börja med en lättare variant, t.ex. att hitta tangenten där x=1.
Kan du få fram den? Då har du en fungerande metod för att ta fram fler tangenter.
Om jag gör det för hand tar jag derivaran av funktionen, stoppar in det aktuelle x-värdet och sedan använder jag mig av en annan punkt för att få ut m-värdet. Finns det något sätt att göra så att geogebra gör detta åt mig?
Ja, den här kräver lite bokföring... och lite gott mod...


Det skall vara y=-x-1. Slarvfel.
Medan 'hansa' skriver följer jag upp med:
Hur visar man snabbt och enkelt att roten ±1/sqrt(3) för
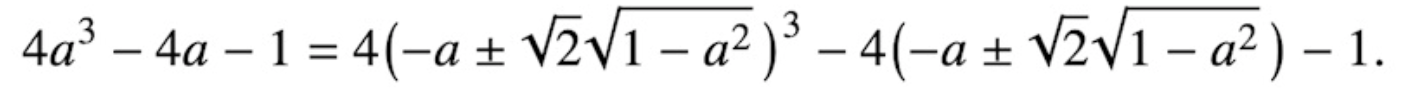
inte är intressant?
y=-1-x skall det väl vara. Geogebra ger en gissning för lutningen -1 som kan verifieras genom att då få
y´=4x3-4x-1=-1 , och därmed x=0,-1 och +1. insättning i funktionen ger för -1 och +1 att den blir 0 och -2. Så linjen mellan punkterna har lutningen -1, som var derivatan i dessa punkter. Fult men med utnyttjande av tipset.
hansa skrev:y=-1-x skall det väl vara. Geogebra ger en gissning för lutningen -1 som kan verifieras genom att då få
y´=4x3-4x-1=-1 , och därmed x=0,-1 och +1. insättning i funktionen ger för -1 och +1 att den blir 0 och -2. Så linjen mellan punkterna har lutningen -1, som var derivatan i dessa punkter. Fult men med utnyttjande av tipset.
Ja, skrivfel av mig.
Trinity2 skrev:amyc skrev:Bubo skrev:Börja med en lättare variant, t.ex. att hitta tangenten där x=1.
Kan du få fram den? Då har du en fungerande metod för att ta fram fler tangenter.
Om jag gör det för hand tar jag derivaran av funktionen, stoppar in det aktuelle x-värdet och sedan använder jag mig av en annan punkt för att få ut m-värdet. Finns det något sätt att göra så att geogebra gör detta åt mig?
Ja, den här kräver lite bokföring... och lite gott mod...
Det skall vara y=-x-1. Slarvfel.
Tack så hemskt mycket! Förstår mycket bättre nu.
amyc skrev:Trinity2 skrev:amyc skrev:Bubo skrev:Börja med en lättare variant, t.ex. att hitta tangenten där x=1.
Kan du få fram den? Då har du en fungerande metod för att ta fram fler tangenter.
Om jag gör det för hand tar jag derivaran av funktionen, stoppar in det aktuelle x-värdet och sedan använder jag mig av en annan punkt för att få ut m-värdet. Finns det något sätt att göra så att geogebra gör detta åt mig?
Ja, den här kräver lite bokföring... och lite gott mod...
Det skall vara y=-x-1. Slarvfel.
Tack så hemskt mycket! Förstår mycket bättre nu.
Kanon. Notera att det finns en lösning till, a=-1/sqrt(3) och jag har ej motiverat varför den inte är aktuell algebraiskt, men man ser direkt på grafen att denna punkt och tillhörande b ej är kandidater.