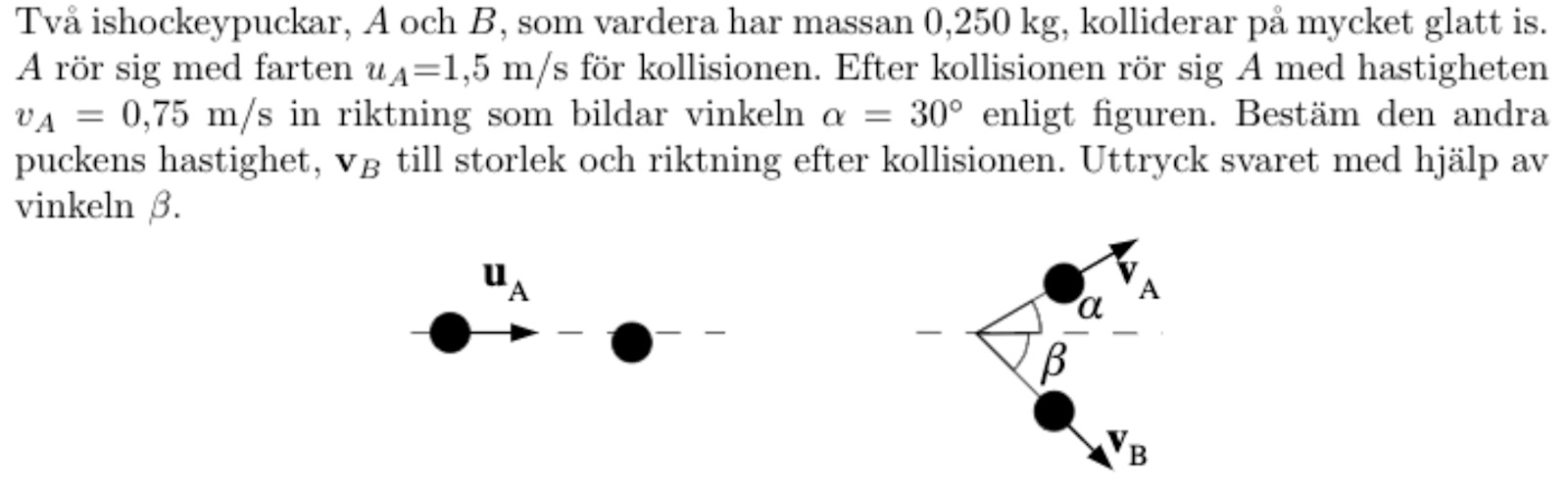
två partiklar som krockar

Rörelsemängden bevaras. Ställ upp ekvationer för det.

Att rörelseenergin bevaras står inte i uppgiften.

Om rörelsemängden bevaras borde det väl vara m_AU_A+0=m_AV_A+m_BV_B

VL: 0.375 om vi räknar ut det numeriskt

Det är ett tvådimensionellt problem och på universitetsnivå ska man normalt använda vektorer. Vet du hur man gör det?

Annars kan du dela upp problemet i x- och y-led. Alltså får du att rörelsemängden i x-led och y-led bevaras. Hantera då dessa separat. I x-led har du exempelvis:

$m u_A = m v_A \cos(\alpha) + mv_B \cos(\beta)$

Du får en ekvation i x-led och en i y-led.

Ebola skrev:

Det är ett tvådimensionellt problem och på universitetsnivå ska man normalt använda vektorer. Vet du hur man gör det?

Annars kan du dela upp problemet i x- och y-led. Alltså får du att rörelsemängden i x-led och y-led bevaras. Hantera då dessa separat. I x-led har du exempelvis:

$m u_A = m v_A \cos(\alpha) + mv_B \cos(\beta)$

Ah okej är med.

Och i y-led blir ekvationen: $0=m{v}_A\sin \alpha -m{v}_B\sin \beta$ ?

haps skrev:

Ah okej är med.

Och i y-led blir ekvationen: $0=m{v}_A\sin \alpha -m{v}_B\sin \beta$ ?

Exakt. Du har nu två ekvationer och två okända så att du kan lösa uppgiften.