Två fjädrar i svängning

Hej!

Du kan försöka hitta en formel för hur man beräknar (dvs vad som bestämmer) svängningsfrekvensen för en harmonisk svängningsrörelse. Ta formelsamlingen till hjälp. Då kommer du att se att k och m är det avgörande. 

Första steget mot att hitta svaret till uppgiften består alltså i att förstå hur fjäderkonstanten $k_{total}$ kommer att se ut om du seriekopplar två fjädrar med fjäderkonstant $k$.

Kommer du vidare? 

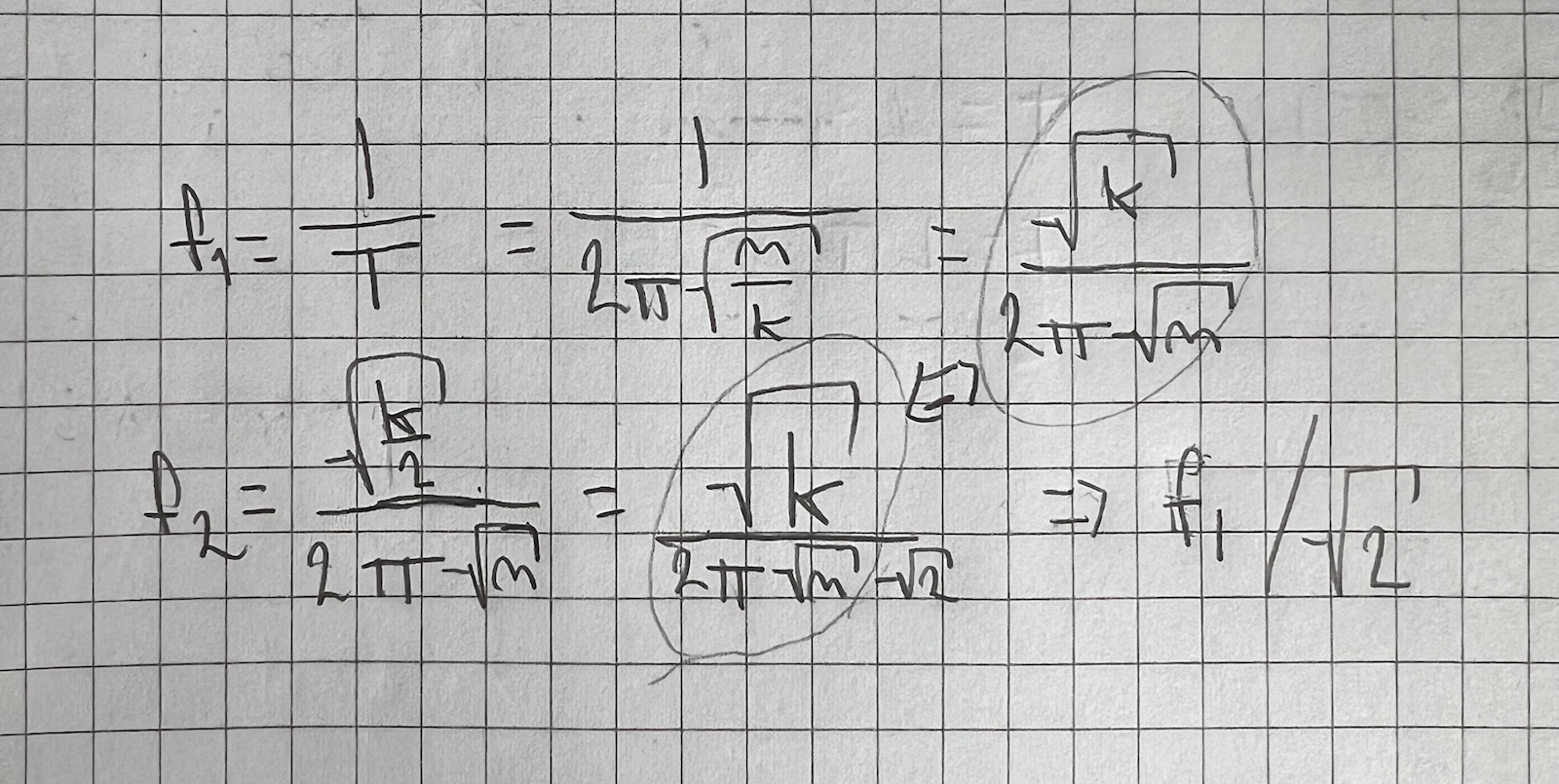
Oki, jag har än så länge kommit fram till att frekvensen, 1/T, kan skrivas som $\frac{\sqrt{k}}{2\mathrm{\pi }\sqrt{\mathrm{m}}}$

Den ges av T = $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

Om vi seriekopplar två fjädrar antar jag att de svänger långsammare

Om vi seriekopplar två fjädrar antar jag att de svänger långsammare

Ja, det gör det. Du måste antingen härleda ett uttryck för $k_{total}$, uttryckt i $k$,eller om du har tur att din lärobok beskriver detta. Sedan kan du relatera $T_{total}=2\pi \sqrt{\frac{m}{k_{total}}}$ med det ursprungliga$T=2\pi \sqrt{\frac{m}{k}}$.

Jag förstår hur du menar och hur man går till väga, fast hur vet jag hur mycket K kommer att minska?

Gör ett tankeexperiment.

En fjäders k-värde beskriver hur mycket kraft som behövs för att dra ut fjädern sträckan $∆x$, enligt Hook's lag $F=k·∆x$. Eller omvänt, hur lång sträcka $∆x$ man kan dra ut en fjäder med hjälp av kraften $F$.

Om man då seriekopplar två fjädrar som har fjäderkonstant $k$, och drar i den totala fjädern med kraften $F$, så kommer varje fjäder att dras ut sträckan $∆x$, dvs den totala utdragningen kommer att bli $2·∆x$.

Alltså,

- Om vi drar ut en av dessa fjädrarna med kraften $F$, så dras den ut sträckan $∆x$.

- Om de två fjädrarna seriekopplas så kan vi plötsligt dra ut den totala fjädern sträckan $2·∆x$, med samma kraft $F$. 

Vad betyder det, om om man ska uttrycka den totala fjäderns $k_{total}$ med hjälp av de individuella fjädrarnas $k$, dvs hur förhåller sig $k_{total}$ till $k$?

Alltså, om jag förstått rätt (din förklaring är jättebra förresten) blir det dubbelt så lätt att förlänga fjädern? Om den enskilda fjädern ska dras ut sträckan Δx, behöver två fjädrar i serie endast dras ut sträckan Δx/2 vardera..?

Följaktligen halveras k-värdet för varje fjäder då de delar på jobbet kan man säga?

Dit resonemang tycker jag ser jättebra ut. Stämde det med facit?

Man kan resonera på liknande sätt om man serie- eller parallellkopplar fjädrar med olika fjäderkonstanter, och komma fram till mer generella formler. Om du är intresserad, kolla till exempel här https://youtu.be/Py7qnXtMIUA?si=EL2ve3L0VR47TeY5

Tack så mycket! I facit står det 0,7f Hz, så det stämmer.

Jag tittade på videon och det påminner om elläran med resistorer. Fast motsatsen

jalsho skrev:

Tack så mycket! I facit står det 0,7f Hz, så det stämmer.

Jag tittade på videon och det påminner om elläran med resistorer. Fast motsatsen

Precis!