Två absolutbelopp i funktion
Hej, jag har suttit fast på en fråga ett tag och har kört fast i början. I uppgiften ska man ta reda på vilket värde x antar vid olika funktionsvärden. Funktionen jag har är:
f(x)=|x+1|-|x-1|
För denna funktion vill jag ta reda på var teckenbyte sker och använder mig av definitionen för absolutbelopp. Nedan infogar jag bild. Ser någon vad jag gör del? Jag gick in på tekniskfysik.org och där har man undersökt x+1<0 och då får de fram de givna intervallen. Jag fattar helt enkelt inte alls varför detta räcker och vad som hände med definitionen för absolutbelopp. Är det något jag har missuppfattat?
Tack på förhand
Du har skrivit nästan rätt.
Följande gäller avseende absolutbelopp:
- då
- då
Det betyder att
- då , dvs då
- då , dvs då
Och att
- då , dvs då
- då , dvs då
Hänger du med så långt?
Hmm jag tror det. Jag har satt att men det man ska göra är att ta den "positiva definitionen" och sätta att den är mindre än noll? Tror jag ser nu var det har blivit konstigt.
Laura2002 skrev:[...] men det man ska göra är att ta den "positiva definitionen" och sätta att den är mindre än noll?
Jag är osäker på vad du menar här.
Vi tar ett annat exempel för att se om du vet hur man gör.
Kan du skriva om uttrycket |x+3| utan absolutbelopptecken och ange var de olika uttrycken gäller?
Absolut, om jag förstår det rätt så får vi
Alltså, om x är lika med -3 eller ett tal som är större än -3 ska vi använda oss utav x+3. Om x däremot är mindre än -3 ska vi använda oss utan -(x+3). Visst blir det rätt då? I min uträkning där uppe har jag multiplicerat in minustecknet och därefter löst ut x vilket är fel
Laura2002 skrev:Absolut, om jag förstår det rätt så får vi
Alltså, om x är lika med -3 eller ett tal som är större än -3 ska vi använda oss utav x+3. Om x däremot är mindre än -3 ska vi använda oss utan -(x+3). Visst blir det rätt då?
Ja, det är rätt!
I min uträkning där uppe har jag multiplicerat in minustecknet och därefter löst ut x vilket är fel
Ja, där blandade du ihop det.
====
Hur lyder själva uppgiften och hur långt kommer du på den nu?
Klarade av den helt och hållet :) Tack för hjälpen!
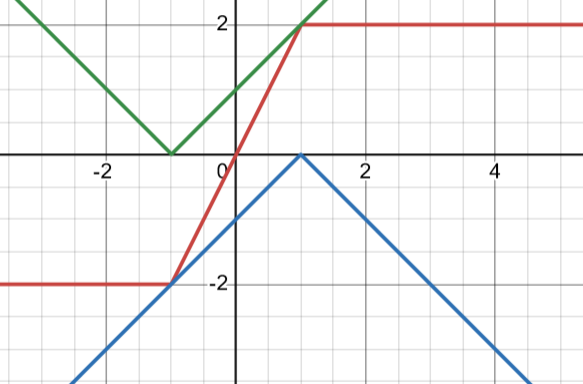
En bild säger mer än tusen ord: