Tryck

Du behöver nog en formel också som talar om vad som händer med luftens volym när trycket ändras.

Laguna skrev:

Du behöver nog en formel också som talar om vad som händer med luftens volym när trycket ändras.

$$\begin{gathered} Höjd av vattennivå: \\ ∆P=1000kg/m^3 \times 9,82 m/s^2 \times 15 m \\ ∆P = 147300 Pa \\ Tryck vid 15 m djup: \\ P total: 101325 Pa + 147300 Pa \\ P total: 248625 Pa \\ h=P total / \rho \times \\ h= 248625 Pa / 1000 kg/m^{3 }\times 9,82 m / s^2 \\ h = 25,3m \end{gathered}$$

tänker jag rätt? 

Almjoh skrev:

Laguna skrev:

Du behöver nog en formel också som talar om vad som händer med luftens volym när trycket ändras.

$$\begin{gathered} Höjd av vattennivå: \\ ∆P=1000kg/m^3 \times 9,82 m/s^2 \times 15 m \\ ∆P = 147300 Pa \\ Tryck vid 15 m djup: \\ P total: 101325 Pa + 147300 Pa \\ P total: 248625 Pa \\ h=P total / \rho \times \\ h= 248625 Pa / 1000 kg/m^{3 }\times 9,82 m / s^2 \\ h = 25,3m \end{gathered}$$

tänker jag rätt? 

Vart är det jag gör fel? 

Du har väl ritat en bild med relevanta data utsatta? 

Om inte, gör det och visa din bild! 

Ture skrev:

Du har väl ritat en bild med relevanta data utsatta? 

Om inte, gör det och visa din bild! 

Det är endast så långt jag förstår.

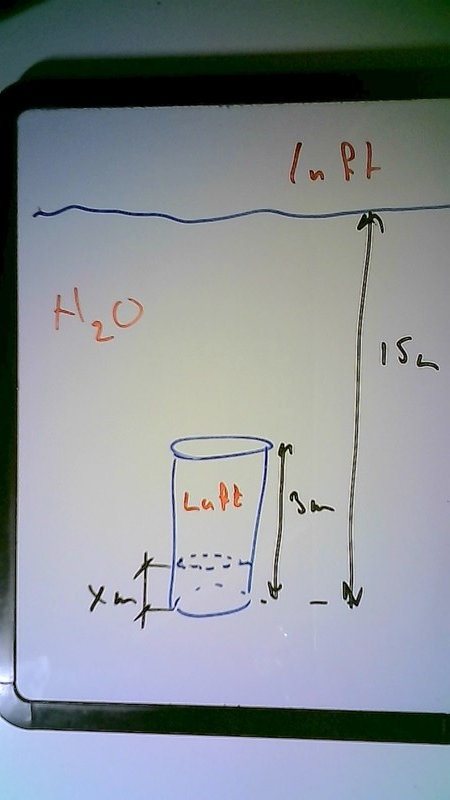
Det finns väl en vattenytan 15 m högre upp, och en vattenytan nånstans inne i cylindern?

Ture skrev:

Det finns väl en vattenytan 15 m högre upp, och en vattenytan nånstans inne i cylindern?

Hur skulle denna vattenytan se ut inne i cylindern?

ungefär så här ser det ut

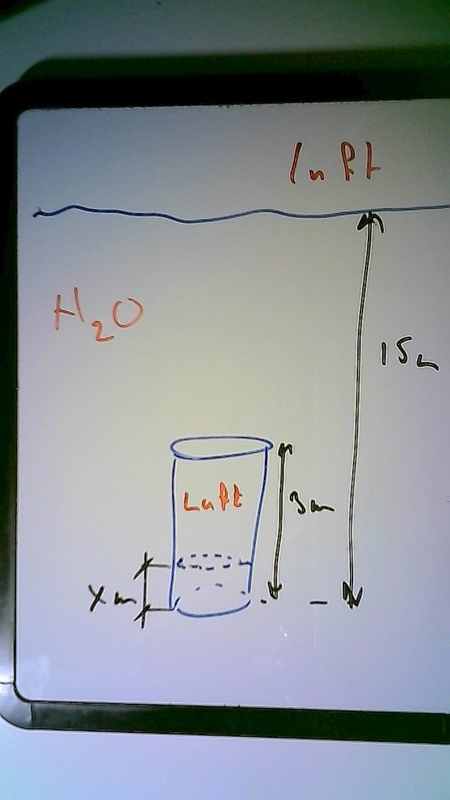
Ture skrev:

ungefär så här ser det ut

 

Tack, hur tar jag mig vidare? Har fastnat på uträkningen vet inte riktigt hur jag ska börja. 

Vattenytan inne i cylindern når till höjden x mätt från cylinderns botten. Hur stort är trycket där? (ett uttryck SOM bl. a innehåller x)

Hur påverkas lufttrycket i cylindern av höjden x? 

Ture skrev:

Vattenytan inne i cylindern når till höjden x mätt från cylinderns botten. Hur stort är trycket där? (ett uttryck SOM bl. a innehåller x)

Hur påverkas lufttrycket i cylindern av höjden x? 

Vet inte om jag tänker rätt men: P = trycket vid djupet, $\rho$= densitet g= tyngdacceleration h= höjd från ytan till djupet 

h=x dvs. P = $\rho \times g\times x?$

Trycket vid djupet är gh*densiteten. 

Trycket vid vattennivån inne i cylindern, x m från cylinderns underkant, hur stort är det? 

Ture skrev:

Trycket vid djupet är gh*densiteten. 

Trycket vid vattennivån inne i cylindern, x m från cylinderns underkant, hur stort är det? 

vet inte, har svårt att komma fram till något rimligt svar. 

Almjoh skrev:

Ture skrev:

Trycket vid djupet är gh*densiteten. 

Trycket vid vattennivån inne i cylindern, x m från cylinderns underkant, hur stort är det? 

vet inte, har svårt att komma fram till något rimligt svar. 

Hur långt under vattenytan är "den inre vattenytan" inuti dykarklockan? Hur stort är vattentrycket på denna nivå?

Smaragdalena skrev:

Almjoh skrev:

Visa föregående citat

Ture skrev:

Trycket vid djupet är gh*densiteten. 

Trycket vid vattennivån inne i cylindern, x m från cylinderns underkant, hur stort är det? 

vet inte, har svårt att komma fram till något rimligt svar. 

Hur långt under vattenytan är "den inre vattenytan" inuti dykarklockan? Hur stort är vattentrycket på denna nivå?

Är det 12 meter? 

Nej, det är botten av dykarklockan, inte vattenytan inuti.

Smaragdalena skrev:

Nej, det är botten av dykarklockan, inte vattenytan inuti.

Om det är botten borde det vara x + 3 = 12 så x=9 eller tänker jag fel? 

Du tänker fel, titta på ritningen och markera i den var vattenytan inuti ligger.  Visa!

Ture skrev:

Du tänker fel, titta på ritningen och markera i den var vattenytan inuti ligger.  Visa!

Javisst! Och avståndet dit från ytan får jag till 15-x meter.

1. Hur stort är då trycket vid det djupet? 

2. Lufttrycket inne i dykarklockan är vid yran 1 bar, vartefter man sänker dykarklockan i vattnet kommer vattennivån inne i klockan att stiga, måttet x ökar. Hur stort är lufttrycket inne i dykklockan som funktion av x?

Ture skrev:

Javisst! Och avståndet dit från ytan får jag till 15-x meter.

1. Hur stort är då trycket vid det djupet? 

2. Lufttrycket inne i dykarklockan är vid yran 1 bar, vartefter man sänker dykarklockan i vattnet kommer vattennivån inne i klockan att stiga, måttet x ökar. Hur stort är lufttrycket inne i dykklockan som funktion av x?

1. $P=\hspace{0.17em}\rho \times g \times (15-x)$? 

2. 1 bar + p x g x (15-x)? 

1. Ditt uttryck för vätsketrycket är ok. 

2. För att beräkna lufttrycket i dykklockan kan du också använda gaslagen, då får du ett annat uttryck som oxå innehåller x, vilket gör dt möjligt att lösa ut x. 

Ture skrev:

Visa spoiler

Skriv ditt dolda innehåll här

 

1. Ditt uttryck för vätsketrycket är ok. 

2. För att beräkna lufttrycket i dykklockan kan du också använda gaslagen, då får du ett annat uttryck som oxå innehåller x, vilket gör dt möjligt att lösa ut x. 

 

Hur gör jag det genom gaslagen? Kan jag inte använda mig av algebra för att göra det: 

$$\begin{gathered} p=\rho \times g\times (15-x) \\ 15-x = \frac{P}{\rho \times g} \\ x = 15 - \frac{P}{p\times g} \end{gathered}$$

Svårigheten med det är att du bara har en ekvation men två obekanta, nämligen x och p.

För att få en ekvation till behöver du använda gaslagen på den instängda luften, vars tryck och volym förändras med ökande värde på x.

Ture skrev:

Svårigheten med det är att du bara har en ekvation men två obekanta, nämligen x och p.

För att få en ekvation till behöver du använda gaslagen på den instängda luften, vars tryck och volym förändras med ökande värde på x.

Så det blir $\frac{nRT}{V_0-A\times x}?$

om vi tittar på dykarklockan så innehåller den en viss mängd luft vid ytan, och trycket är atmosfärstrycket, när vi sänker ned den i vattnet minskar volymen och trycket ökar, men mängden luft (antal molekyler) är oförändrad. Vi antar att luftens temperaturen i klockan är oförändrad.

Gaslagen säger att PV = nRT där nRT är oförändrade i det här fallet så vi kan förenkla det till

PV = k, där k är en konstant

Alltså gäller 

(PV)_ytan = (PV)_15-x

Det du ska göra nu är att bestämma hur V och därmed P beror av x

Ture skrev:

om vi tittar på dykarklockan så innehåller den en viss mängd luft vid ytan, och trycket är atmosfärstrycket, när vi sänker ned den i vattnet minskar volymen och trycket ökar, men mängden luft (antal molekyler) är oförändrad. Vi antar att luftens temperaturen i klockan är oförändrad.

Gaslagen säger att PV = nRT där nRT är oförändrade i det här fallet så vi kan förenkla det till

PV = k, där k är en konstant

Alltså gäller 

(PV)_ytan = (PV)_15-x

Det du ska göra nu är att bestämma hur V och därmed P beror av x

V och P ska vara proportionella så när volymen ökar så minskar trycket och vice versa. Så när x ökar kommer volymen av luften i dykarklockan öka, och då kommer trycket att minska. fattar dock inte hur jag ska skriva detta. 

När Dykarklockan sänks ned i vattnet kommer den inneslutna luftens volym att minska, inte öka.

Innan dykarklockan sänks ned i vattnet, vilket tryck har luften i den och vilken volym? 

När dykarklockan sänkts ned i vatten och vatten trängt in underifrån till höjden x från undre kanten, vilken volym har den instängda luften då? 

Ture skrev:

När Dykarklockan sänks ned i vattnet kommer den inneslutna luftens volym att minska, inte öka.

Innan dykarklockan sänks ned i vattnet, vilket tryck har luften i den och vilken volym? 

När dykarklockan sänkts ned i vatten och vatten trängt in underifrån till höjden x från undre kanten, vilken volym har den instängda luften då? 

Innan den sänks ned i vattnet borde trycket vara 1 bar. Har svårt att komma fram till något angående volym eller när den sänks ned i vattnet. 

nog vet du väl hur man beräknar volymen av en cylinder??

Ture skrev:

nog vet du väl hur man beräknar volymen av en cylinder??

Jo, inann den sänks ned till vattnet bör det vara ≈ 9,42 m^3

så när som på enheten är det rätt, m³ ska det vara.

Och om det är vatten x meter upp i cylindern, hur stor är då återstående volym?

Ture skrev:

så när som på enheten är det rätt, m³ ska det vara.

Och om det är vatten x meter upp i cylindern, hur stor är då återstående volym?

$\mathrm{\pi }\times (2-\mathrm{x}) {\mathrm{m}}^3$?

Läs uppgiften noga, skissa cylindern och försök igen. 

Ture skrev:

Läs uppgiften noga, skissa cylindern och försök igen. 

Jag förstår fortfarande inte riktigt, menar du kanske att 15-x ska vara med i uträkningen? Eftersom det är 15-x som är uppfyllt med vatten. 

Nej, kolla siffrorna i ditt förra inlägg! 

Ture skrev:

Nej, kolla siffrorna i ditt förra inlägg! 

$\pi \times (3-x) m^3$?

Japp!

Hur blir det då med gaslagen? 

Ture skrev:

Japp!

 

Hur blir det då med gaslagen? 

Tycker du svaret verkar rimligt? 

Ture skrev:

Tycker du svaret verkar rimligt? 

Med tanke på att hela cylindern är 3 m hög  så är det väldigt nära 3m så troligen inte. Men vet inte vart felet är. 

Bra att du inser det, nånstans runt 1,7 till 1,9 m tycker jag känns mer rimligt. 

Jag kollar i morgon

Du måste använda rätt enheter när du räknar, SI enheter rakt igenom rekommenderas starkt! Jag har inte kollat i detalj vad du gör, det är svårt att följa dina beräkningar,  men du verkar använda kg/liter för vattnets densitet, det ska vara kg/m³.

För gasen i dykarklockan gäller enligt gaslagen

P₀V₀ = PV  (Där P och V är tryck resp volym i nedsänkt läge och P₀ och V₀ gäller före nedsänkning)

Sätter vi in de siffror vi har får vi (x är den sökta vattennivån inne i dykarklockan)

$$\begin{gathered} P_0*\pi *1^2*3 =\hspace{0.17em}P*\pi *1^2*(3-x) \Rightarrow \\ \mathit{P}\mathbf{ }\mathbf{=}\mathbf{\hspace{0.17em}} \frac{{\mathbf{P}}_{\mathbf{0}}\mathbf{*}\mathbf{3}}{\mathbf{(}\mathbf{3}\mathbf{-}\mathbf{x}\mathbf{)}} \end{gathered}$$ 

För vattnet gäller på djupet 15-x, (g är tyngdacceledrationen , $\rho$ är vattnets densitet)

$\mathit{P}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{\rho }\mathit{g}\mathbf{(}\mathbf{15}\mathbf{-}\mathit{x}\mathbf{)}\mathbf{ }\mathbf{+}{\mathit{P}}_{\mathbf{0}}$

eftersom det är samma P i bägge ekvationerna kan vi sätta

$\rho g(15-x) + P_0=\frac{{\mathrm{P}}_0*3}{(3-\mathrm{x})}$

med siffror ($\rho$ = 1000 kg/m³ , g = 9,82 kgm/s² , P₀ = 10⁵ N/m² )

${10}^3*9,82(15-x) +{10}^5 =\frac{3*{10}^5}{3-x}$, (en andragradsekvation att lösa, två lösningar och vi måste välja den rätta)

vilket jag får till att x = cirka 1,7 m 

Ture skrev:

Du måste använda rätt enheter när du räknar, SI enheter rakt igenom rekommenderas starkt! Jag har inte kollat i detalj vad du gör, det är svårt att följa dina beräkningar,  men du verkar använda kg/liter för vattnets densitet, det ska vara kg/m³.

För gasen i dykarklockan gäller enligt gaslagen

P₀V₀ = PV  (Där P och V är tryck resp volym i nedsänkt läge och P₀ och V₀ gäller före nedsänkning)

Sätter vi in de siffror vi har får vi (x är den sökta vattennivån inne i dykarklockan)

$$\begin{gathered} P_0*\pi *1^2*3 =\hspace{0.17em}P*\pi *1^2*(3-x) \Rightarrow \\ \mathit{P}\mathbf{ }\mathbf{=}\mathbf{\hspace{0.17em}} \frac{{\mathbf{P}}_{\mathbf{0}}\mathbf{*}\mathbf{3}}{\mathbf{(}\mathbf{3}\mathbf{-}\mathbf{x}\mathbf{)}} \end{gathered}$$ 

 

För vattnet gäller på djupet 15-x, (g är tyngdacceledrationen , $\rho$ är vattnets densitet)

$\mathit{P}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{\rho }\mathit{g}\mathbf{(}\mathbf{15}\mathbf{-}\mathit{x}\mathbf{)}\mathbf{ }\mathbf{+}{\mathit{P}}_{\mathbf{0}}$

eftersom det är samma P i bägge ekvationerna kan vi sätta

$\rho g(15-x) + P_0=\frac{{\mathrm{P}}_0*3}{(3-\mathrm{x})}$

med siffror ($\rho$ = 1000 kg/m³ , g = 9,82 kgm/s² , P₀ = 10⁵ N/m² )

${10}^3*9,82(15-x) +{10}^5 =\frac{3*{10}^5}{3-x}$, (en andragradsekvation att lösa, två lösningar och vi måste välja den rätta)

vilket jag får till att x = cirka 1,7 m 

Varför blir $P_0={10}^{5}N/m^2?\hspace{0.17em}$

Varför blir P₀=10⁵ N/m²? 

Vad är normalt lufttryck?