Tröghetsmoment som funktion av vinkel
Hej!
Försöker få ihop denna:
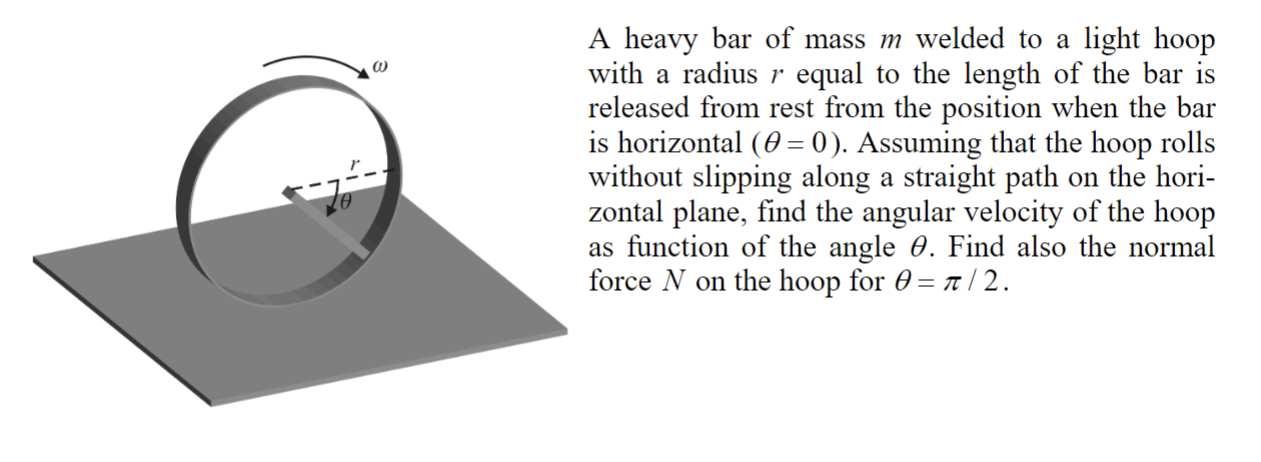
Men av någon orsak blir ingenting rätt. Har testat att ta tröghetsmomentet i masscentrum, har även testat ta tröghetsmomentet i mitten på cirkeln samt i den lägsta punkten på cirkeln för att sedan använda energisambandet och få ihop et uttryck för omega, men får inte alls rätt svar.
Har tänkt såhär:
Tröghetsmomentet, stång:
Parallellförflyttningssatsen till cirkelns lägsta punkt, C:
Hastigheten i C:
Energisambandet:
Nu om man bryter ut omega får man inte alls att
Någon som kan ge tips på hur frågan ska lösas?
Tack!
Du kan se rörelsen som sammansatt av två rörelser. En rotation kring masscentrum samt en translation av masscentrum.
Den mekaniska energin är bevarad.
, där
Lös ut
Lämpligt delsteg: Vad blir lägesvektorn för tyngdpunktscentrum? Vad blir absolutbeloppet av dess derivata i kvadrat, dvs ?
D4NIEL skrev:Du kan se rörelsen som sammansatt av två rörelser. En rotation kring masscentrum samt en translation av masscentrum.
Den mekaniska energin är bevarad.
, där
Lös ut
Lämpligt delsteg: Vad blir lägesvektorn för tyngdpunktscentrum? Vad blir absolutbeloppet av dess derivata i kvadrat, dvs ?
Oj, men jo precis, här är en annan liknande metod jag testat:
Har suttit planet som cirkeln rullar på som y=0, därför ges , då jag väljer att sätta , , och ges
Tror att det kan vara här jag får problem, använder hastighetssambandet för en stel kropp: , där , här ges sedan hastigheten i G som:
Sedan sätter jag in i formeln för den mekaniska energin jag tagit fram, då blir vinkelhastigheten ändå inte rätt...
Jag vet inte om jag tolkar dig rätt, men masscentrum följer den blå linjen nedan och rör sig inte bara i en cirkelbåge utan också åt höger i bild.

Den hastighet du tagit fram är bara vinkelhastigheten runt cirkelcentrum, inte translationen. Dessutom är den effektiva radien . Om du lägger till translationshastigheten får du nästan rätt.
Förövrigt, hur får du och ?
Om är den potentiella energin i ett senare läge ges den som funktion av och är
Den är aldrig noll om .
D4NIEL skrev:Jag vet inte om jag tolkar dig rätt, men masscentrum följer den blå linjen nedan och rör sig inte bara i en cirkelbåge utan också åt höger i bild.
Den hastighet du tagit fram är bara vinkelhastigheten runt cirkelcentrum, inte translationen. Dessutom är den effektiva radien . Om du lägger till translationshastigheten får du nästan rätt.
Förövrigt, hur får du och ?
Om är den potentiella energin i ett senare läge ges den som funktion av och är
Den är aldrig noll om .
Hm, men tar ju med både ban och spinn-delen av den mekaniska energin, dvs. ger väl den totala hastigheten för punkten i fråga (masscentrum?), jag tog som hastigheten för den punkt på cirkeln som sitter närmast planet, och hastigheten för den punkten är =0.
Menar du att man borde ta fram hastighetssambandet för stångens mittpunkt med hjälp av translationshastigheten för cirkelns mittpunkt istället? Isåfall kan jag förstå hur det ger ett annat resultat, ja.
När det kommer till den potentiella energin såg ditt svar absolut mer rätt ut! Tror att jag är lite förvirrad över vilka punkter man ska använda i beräkningarna, man ska alltså räkna fram stångens masscentrums hastighet, tröghetsmoment och potentiell energi och sätta in i "formeln"?
Det är ju lite olika tankesätt, och jag rekommenderar att du räknar som ni lärt er. Du måste inte tänka på det som "translation + rotation"
Men är inte Vektorn som talar om var tyngdpunkten befinner sig i förhållande till kontaktpunkten C?
Då är den
Jämför med vårt förväntade resultat när
Vidare är jag inte med på din kryssprodukt. Med , vi roterar ju medurs, får vi
Vilket ger dig den korrekta hastigheten. Så man kan ju räkna på det sättet också, om man räknar rätt...
D4NIEL skrev:Det är ju lite olika tankesätt, och jag rekommenderar att du räknar som ni lärt er. Du måste inte tänka på det som "translation + rotation"
Men är inte Vektorn som talar om var tyngdpunkten befinner sig i förhållande till kontaktpunkten C?
Då är den
Jämför med vårt förväntade resultat när
Vidare är jag inte med på din kryssprodukt. Med , vi roterar ju medurs, får vi
Vilket ger dig den korrekta hastigheten. Så man kan ju räkna på det sättet också, om man räknar rätt...
Jättetack, känner att jag hänger med bättre nu!
Undrar däremot hur du kom fram till , mer specifikt y-komponenten?
Har försökt sätta ihop något liknande ett tag, men kom aldrig fram till något vettigt.
Insåg nu när du skrev det att jag suttit positiv z-axel åt fel håll, tack för påpekandet! :)
y-komponenten får man fram med trigonometri, till exempel en rätvinklig triangel. Var inte rädd för att rita bilder och ta fram uttryck för masscentrum och andra punkter. När man gjort det några gånger blir det lättare.

Hypotenusans längd till masscentrum är . Alltså blir det markerade vertikala avståndet (kateten) och höjden över x-axeln därmed .
D4NIEL skrev:y-komponenten får man fram med trigonometri, till exempel en rätvinklig triangel. Var inte rädd för att rita bilder och ta fram uttryck för masscentrum och andra punkter. När man gjort det några gånger blir det lättare.
Hypotenusans längd till masscentrum är . Alltså blir det markerade vertikala avståndet (kateten) och höjden över x-axeln därmed .
Testade att sätta in det övre i energisambandet och får :
, satte in och , vet inte om jag missförstått något?
Jag tror att du blandar ihop våra betraktelsesätt nu, jag borde bett dig redovisa dina räkningar från början så hade vi kunnat fokusera på rörelse kring fix punkt C, dvs .
Hastigheten blir
Hastigheten i kvadrat (dvs normen i kvadrat), dvs det vi behöver till vår rörelseenergi är därmed
Energisambandet som du använder är med :
Sätter vi in våra resultat och värden får vi
Lös ut

