Tröghetsmoment smal stav
En smal stav med längden 𝑙 och massan 𝑚m ligger i 𝑥𝑦-planet, och bildar vinkeln 𝛽 med 𝑥-axeln. Bestäm dess tröghetsmoment runt masscentrum m.a.p. rotation runt 𝑥- 𝑦- och 𝑧-axlarna.
Jag har försökt lösa uppgiften både med direkt integration och genom steiners sats [I0 =Ig+md^2]. Får vid båda fall att svaret ska vara ml^2cos^2(beta)/3. Facit vill ha en nämnare 12, vilket skulle vara detsamma som att jag betraktar staven som en punktmassa (formeln ml^2).
Var har det gått snett i min tanke? Nedan är både uppgiften och mitt försök till lösningar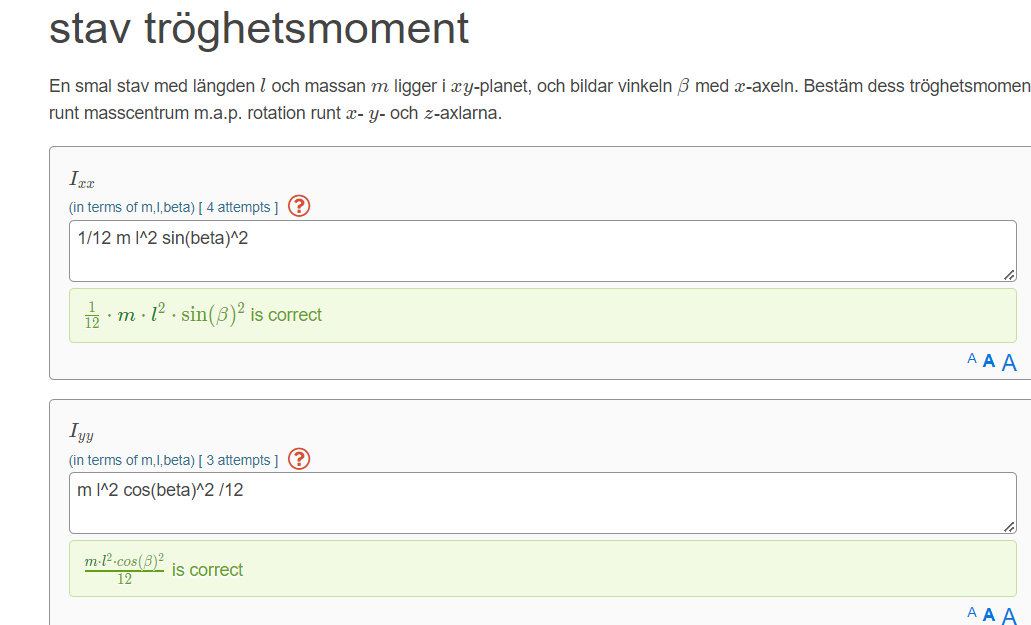

Hade inte läst frågan ordentligt (trodde de ville ha trögheten kring ena änden och inte masscentrum). Löste sig
Det står att du skall lösa uppgiften medelst rotation kring axlarna. Var gör du det i din lösning?
Jag visade bara lösning för y-axel. Vet inte om du syftar på att lösningen är slarvigt utförd men tröghetsmomentet kring y medelst en rotation kring y är Iy=1/12 * ma^2 där a är stavens längd i x-led.
Jag tänkte att man kanske skulle lösa uppgiften med rotationsmatriser och inte integration. Men jag kanske övertolkade det som du skrev.


