Tröghetsmoment och masscentrum (Matematik/Universitet)

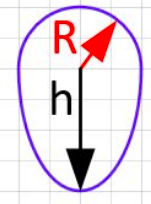
Är den undre halvan en parabel?

Är all massa belägen ute vid randen?

Tillägg: 18 dec 2021 15:41

Gissar istället att den undre delen är en halv ellips.

Den nedre delen tolkar jag som en halv ellips. Det är ett tvärsnitt på en balk, så figuren är massiv. Balken har massan 100kg.

Ok, börja med att hitta masscentrum i y-led. Kanske blir det enklast att dela in området i horisontella remsor.

Yes gjort det, delat upp respektive del och får masscentrum för halvcirkel (0,121) samt halv ellips (0,66). Placerat koordinatsystemet med Y-axeln i mitten. Tips på hur jag kan gå vidare? :)

Om du har två kända massor med kända masscentra så blir systemets masscentrum ...

Jo jag vet hur masscentrum för systemet kan räknas ut. Men är tröghetsmomentet jag behöver integrera. Behövs systemets masscentrum för att göra den typ av beräkning? Hittar nämligen inte något om det. Det jag hittar är att Ix=integralen av (y^2dA), vilket går att beräkna utan masscentrum vad jag förstår det som. Mitt problem nu är väl helt enkelt hur man gör den typ av beräkning.

Det är nog enklast att beräkna tröghetsmomenten m.a.p diametern/ellipsens lillaxel och sedan flytta till masscentrum med steiners sats.

Men hela uppgiften handlar om integraler så måste dessvärre integrera fram I...

Hur ser integralen då ut om du försöker integrera med brute force?

Får det till Ix=5787702,3mm^4 samt Iy=10245037,5mm^4

X-axeln går där den svarta och röda pilen möts, alltså där ellips övergår till cirkel. Y axeln går genom mitten.

Låter detta rimligt?

Ekvation för cirkel:

$x^2+y^2 = R^2$

Ellips:

$x^2/R^2+y^2/h^2=1$

Tröghetsmoment:

$I_x=\displaystyle \int y^2 dA$

$I_y=\displaystyle \int x^2 dA$

Det jag hittar är att Ix=integralen av (y^2dA), vilket går att beräkna utan masscentrum vad jag förstår det som. Mitt problem nu är väl helt enkelt hur man gör den typ av beräkning.

Du måste veta tyngdpunkten då det är i denna du lägger koordinataxlarna du relaterar momentet till. Annars hade problemet angett vilken specifik axel du ska beräkna relativt. För ett tvärsnitt är det neutralaxlarna vid den geometriska tyngdpunkten som är intressant. Det är denna som åsyftas när du beräknar spänning exempelvis:

$\sigma_z = \dfrac{M\cdot y}{I_x}$

X-axeln går där den svarta och röda pilen möts, alltså där ellips övergår till cirkel. Y axeln går genom mitten.

Låter detta rimligt?

Du kan inte veta säkert var tyngdpunkten är belägen utan måste beräkna det. Den ligger absolut inte där den röda och svarta pilen möts. Det skulle den bara göra om $R = h$ men $R = h/2$ .

Du beräknar var den ligger med:

$\displaystyle \bar{x} = \int x f\left(x\right)dx$

$\displaystyle \bar{y} = \int y f\left(y\right)dy$

Du har funktionerna genom ekvationerna för ellips och cirkel.

Jag placerade koordinatsystemet där för att få enklare beräkningar då jag kan räkna på en halvcirkel och en halv ellips. Sålänge de är i samma koordinatsystem så kan de sedan adderas för att få tröghetsmomentet för figuren. Placerar jag systemet i tyngdpunkten så blir beräkningarna betydligt mycket mer komplicerade.

Men det är inte möjligt att räkna på det sättet och sedan prallellförflytta till tyngdpunkten mha steiners sats?

Tyngdpunkten ligger vid 84,3 i Y-led. Hur går jag vidare härifrån?

saan98 skrev:
Jag placerade koordinatsystemet där för att få enklare beräkningar då jag kan räkna på en halvcirkel och en halv ellips. Sålänge de är i samma koordinatsystem så kan de sedan adderas för att få tröghetsmomentet för figuren. Placerar jag systemet i tyngdpunkten så blir beräkningarna betydligt mycket mer komplicerade.

Helt rätt. Bra tänkt. Jag trodde du menade att tyngdpunkten låg där.

Men det är inte möjligt att räkna på det sättet och sedan prallellförflytta till tyngdpunkten mha steiners sats?

Jo, absolut. Räkna ut tröghetsmomentet för en halv cirkel och en halv ellips (hälften av för en hel cirkel eller hel ellips) samt deras respektive centroider. Använd sedan Steiners till hela tvärsnittets tyngdpunkt.

Tyngdpunkten ligger vid 84,3 i Y-led. Hur går jag vidare härifrån?

Vad menar du när du skriver så? Om du satt ditt koordinatsystem där du skrev ligger y = 84.3 utanför tvärsnittet. Varför är annars y positiv nedåt? Kan du visa hur du har räknat och rita en figur?

När tyngdpunkten blir 84,3 så satte jag koordinatsystemets x-axel längst ned på figuren och Y-axeln i mitten. Förstår att det är svårt att hänga med i mina beräkningar, testar mg fram på olika sätt.. Ber om ursäkt för det!

Men tror att jag kör på första alternativet, att jag beräknar tröghetsmomentet för respektive del och sedan adderar!

Det finns inget att ursäkta. Jag ville bara se hur du hade tänkt.

Om du sätter x-axeln vid undersidan av halvcirkeln (eller ovansidan på halvellipsen) med y-axeln riktad uppåt mot cirkelns toppsida är avståndet till gemensamma tyngdpunkten:

$\bar{y} = - \dfrac{200}{3\pi} \approx -21.2$

Från nederkanten är alltså avståndet till gemensamma tyngdpunkten:

$\bar{y}* = 100 -\dfrac{200}{3\pi} \approx 78.8$

Detta beräknas enklast med diskretisering av ursprungliga integralen för centroid:

$\displaystyle \bar{y} = \dfrac{\sum y_i A_i}{\sum A_i}$

Där alltså exempelvis för halvcirkeln:

$A_1 = \dfrac{\pi R^2}{2}$

$y_1 = \dfrac{4R}{3\pi}$

Obs: Här är $y_1$ mätt vertikalt upp från punkten där den svarta och röda pilarna utgår.

Är det möjligt att beräkna halvellipsen som en parabel f(x)=0,04x^2-100? Ger en betydligt enklare funktion att integrera.

Om man tänker då att X-axeln är där den svarta och röda pilen möts.

saan98 skrev:
Är det möjligt att beräkna halvellipsen som en parabel f(x)=0,04x^2-100? Ger en betydligt enklare funktion att integrera.

Nej. Som du ser på nedan bild är en parabel (svart) enbart en approximation av en ellips (röd):

Vad tillhör uppgiften för kurs? Är det verkligen matematik? Om det är fysik/mekanik/hållfasthetslära kan du väl bara slå upp integralen i en tabell. Annars är den inte särskilt komplicerad egentligen men även om det är en matematik-kurs ska du inte behöva integrera om det inte står i uppgiften: "Använd integraler för att beräkna...". Att diskretisera som en summa bör räcka.

Oavsett vad, visa hur du ställer upp integralen.

Kursen är hållfasthetslära. Tyvärr måste vi använda integral det är angivet.

Okej. Men du behöver inte beräkna något. Du kan slå upp den i tabell.

Integralen för ellipsen är av denna typ:

$\displaystyle \int y \sqrt{1-y^2/h^2} \ dy$

Denna slår du enkelt upp i valfri tabell eller löser med substitution. Visa hur du ställer upp integralen!

Jag fick en r^2 i min integral, varför fick inte du det?

saan98 skrev:
Jag fick en r^2 i min integral, varför fick inte du det?

Det är bara en konstant som kan flyttas utanför integralen. Du ska ha en faktor 2 också.

Visa din uppställning av integralen.

$I y = 100^2 \int_{- 100}^{0} x^2 * \sqrt{1 - (X^2 / 50^2)} d y$

Vilket inte går att beräkna då det blir negativt under rottecknet..

Det är nära men inte riktigt korrekt. Du verkar ha en del missförstånd. Jag återkommer med en fullständig redogörelse för hur du bör göra.

Tills dess. Fundera på att uttrycket för tyngdpunkten är:

$\displaystyle \bar{y} = \dfrac{\int y \ dA}{\int \ dA}$

Vad är $dA$ för halvellipsen? För halvcirkeln?

Okej tack! Tyngdpunkten har jag integrerat fram och fått samma som du fick ovan, så är endast problemet med tröghetsmomentet kvar..

Mm, du kan se ditt tvärsnitt som detta:

Alltså får vi ett tröghetsmoment runt tyngdpunkten för tvärsnittet som:

$\displaystyle I_x = \int y^2 dA$

Vi får alltså två integraler:

$\displaystyle \int_a^b (f\left(x\right))^2 dA_e + \int_c^d (g\left(x\right))^2 dA_c$

Frågan är vad $a,b,c,d, dA_e, dA_c$ är lika med?

Edit: Rättade till integranden till kvadraten av funktionerna.

Tusen tack!

Då Ix ska beräknas så har jag tolkat det som att det är integrationsgränserna i X-led som motsvarar a och b, alltså -50 och 50. Vilket då även borde motsvara c och d? Och för Iy så är det integrationsgränserna på y-axeln för respektive kurva.

dAe har jag tolkat som en liten massa i den hela figuren, alltså en area, vilket kan skrivas x*dy. Då x motsvarar avståndet i x-led och dy höjden, vilken är så liten att den kan försummas. Vilket jag då tolkar som är detsamma för dAc.

Har jag fått detta om bakfoten?

För att sedan beräkna x*dy så har jag helt enkelt löst ut x ur önskad funktion. Exempelvis Y=x^2 blir då $\sqrt{y}$ =x. Ersätter då x och får $\sqrt{y}$ *dy

saan98 skrev:
Tusen tack!

Då Ix ska beräknas så har jag tolkat det som att det är integrationsgränserna i X-led som motsvarar a och b, alltså -50 och 50. Vilket då även borde motsvara c och d? Och för Iy så är det integrationsgränserna på y-axeln för respektive kurva.

Det är tvärtom. När du exempelvis roterar kring x-axeln är det materialet bort ifrån (längs y-led) som bidrar till tröghetsmomentet.

Ellips-delen

$a=\dfrac{200}{3\pi}-100$

$b = \dfrac{200}{3\pi}$

$dA_e =?$

Cirkel-delen

$c=?$

$d=?$

$dA_c=2xdy=2\sqrt{50^2-\cancel{\color[rgb]{1.0, 0.0, 0.0}2}(y-\frac{200}{3\pi})^2}dy$

Som du ser blir det ganska omständligt och framförallt extremt onödigt att lösa det med en integral för hela tvärsnittet. Får du inte ens använda Steiners sats? Vad exakt står det i uppgiften? Extremt okarakteristiskt och verklighetsfrånvänt att ni måste integrera allt.

dAe har jag tolkat som en liten massa i den hela figuren, alltså en area, vilket kan skrivas x*dy. Då x motsvarar avståndet i x-led och dy höjden,

Nje, du har $2xdy$ därför att du har material både över och under y-axeln, inte sant?

Tillägg: 20 dec 2021 00:26

Det smög in en 2:a i infinitesimalen $dA_c$ som inte ska vara där.

Tack för all hjälp, nu tror jag att jag förstår. Ja integraler blir väldigt krångligt. Vi skriver en beräkningsrapport där vi ska beräkna knäckningsfall på en balk med detta tvärsnitt. Uppgiften har läraren endast gått igenom på tavlan och sagt att vi ska lösa analytiskt mha integraler..

Det som är bra är att du/ni kan alltid kontrollera ert svar med ett CAD-program.

Jag får hursomhelst följande totala integral:

$\displaystyle I_x= 2R\int_{\bar{y}-h}^{\bar{y}} y^2 \sqrt{1-\dfrac{1}{h^2}(y-\bar{y})^2} \ dy + 2R\int_{\bar{y}}^{\bar{y}+R} y^2 \sqrt{1-\dfrac{1}{R^2}(y-\bar{y})^2} \ dy$

Där alltså $\bar{y}=4R/3\pi$ . Här finns det en del saker ni kan göra för att göra integralen enklare att beräkna för hand.

Lycka till!

Tillägg: 20 dec 2021 13:56

Jag tror förövrigt nog att det du föreslog är enklare. Alltså att beräkna tröghetsmomentet för halvcirkel/halvellips var för sig och sedan flytta till tvärsnittets tyngdpunkt med Steiners.