Masströghetsmoment; kasta upp en bok med olika rotationsaxlar
Har sett på följande video om tröghetsmoment: https://www.youtube.com/watch?v=uyU25DdONjo, där detta exempel ges:

Vid kast 1 roteras boken med rotationsaxel vid masscentrum och vid kast 2 roteras boken med bokryggen som rotationsaxel. Dessa 2 rotationer har lätt att förbli stabila under banan som följer kastet.
Kast 3 däremot kommer att rotera kring ena kortsidan, vilket gör att boken mycket lättare roterar hejvilt och inte kring den initiella axeln. Hur kommer det sig att detta sker?
Jag tänker mig att masströgheten är mindre kring axlarna vid kast 1 och 2, och därför är boken mer benägen att i kast 3 rotera kring dom axlarna vid minsta initiella felrotering. Formler för masströghetsmoment är givna i vår formelsamling:
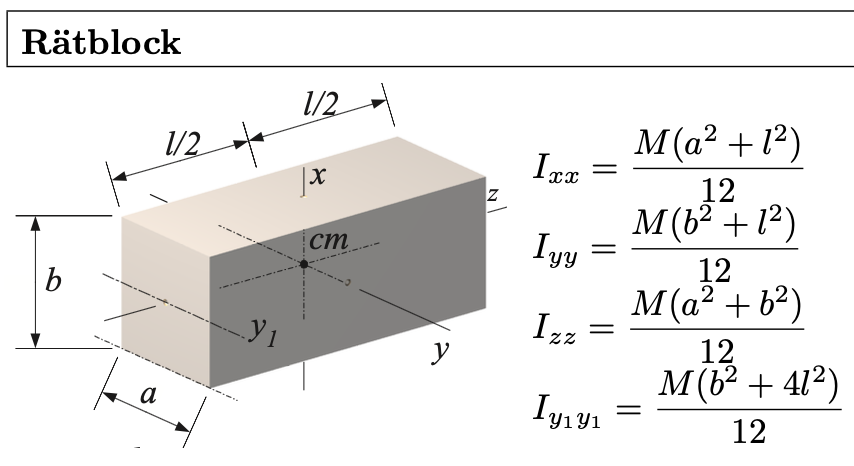
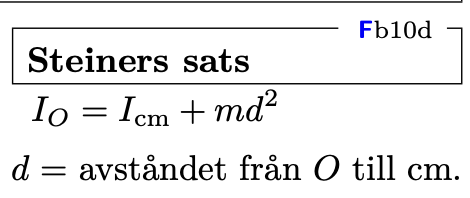
Dessa formler använder jag för respektive kast
Ikast
(Steiners sats)
Och testade genom att sätta in värden för massa, längd och bredd.
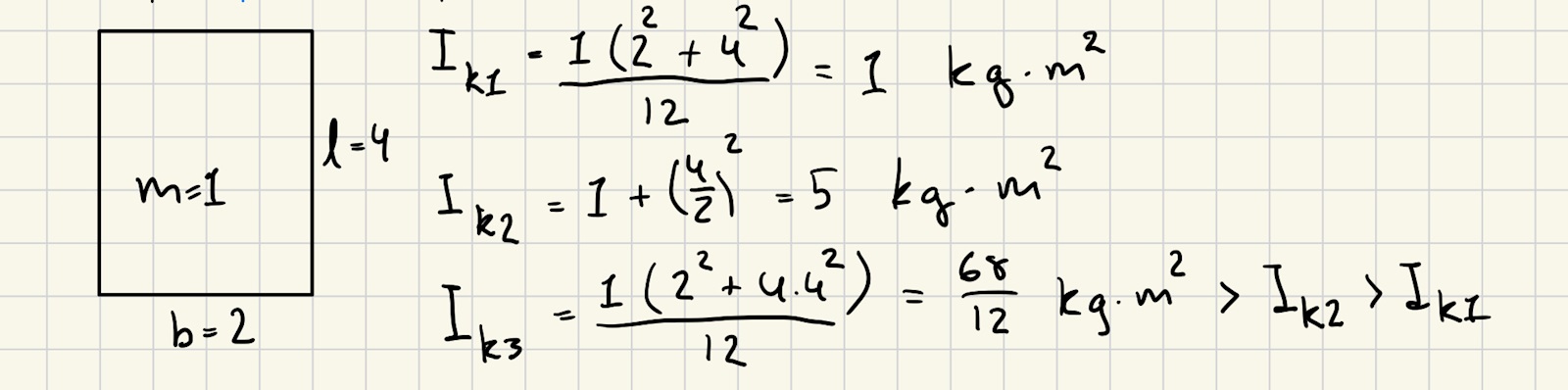
Först och främst, har jag tänkt och gjort rätt för att komma fram till mitt svar?
Detta är om rätt bevisat genom att testa värden, gå det att göra ett bevis för detta utan att sätta in testvärden?
Elias Sk skrev:Har sett på följande video om tröghetsmoment: https://www.youtube.com/watch?v=uyU25DdONjo, där detta exempel ges:
Vid kast 1 roteras boken med rotationsaxel vid masscentrum och vid kast 2 roteras boken med bokryggen som rotationsaxel. Dessa 2 rotationer har lätt att förbli stabila under banan som följer kastet.
Kast 3 däremot kommer att rotera kring ena kortsidan
Vid alla tre kast sker rotationen kring axlar genom masscentrum.
Detta är stelkroppsdynamik och har behandlats av Euler. Det är inte alls särskilt intuitivt.
Pieter Kuiper skrev:Elias Sk skrev:Har sett på följande video om tröghetsmoment: https://www.youtube.com/watch?v=uyU25DdONjo, där detta exempel ges:
Vid kast 1 roteras boken med rotationsaxel vid masscentrum och vid kast 2 roteras boken med bokryggen som rotationsaxel. Dessa 2 rotationer har lätt att förbli stabila under banan som följer kastet.
Kast 3 däremot kommer att rotera kring ena kortsidan
Vid alla tre kast sker rotationen kring axlar genom masscentrum.
Detta är stelkroppsdynamik och har behandlats av Euler. Det är inte alls särskilt intuitivt.
oh juste, rotationsaxeln hamnar ju inte i kanten bara för att han släpper den från kanten 😅
Vi har inte gått igenom Euler, skulle tro som du antyder på att det är lite över fysiken jag läser nu.
Tänkte fel på mina rotationsaxlar, men den har ju fortfarande olika rotationsaxlar där tröghetsmomentet är olika då man använder olika datan till de olika tröghetsmomenten.
Alltså att
Eller är det helt enkelt att fysiken kring detta är kopplat till tröghetsmoment, men att man behöver eulers formler för att beskriva det?
En bok är bara ungefär ett rätblock. I ett koordinatsystem med dessa riktningar får nog tröghetstensorn fler element som inte är noll än på diagonalen. Så det blir jobbigt.
Mer än så vet jag inte.



