Tröghetsmoment för stav kring punkt ej centrerad

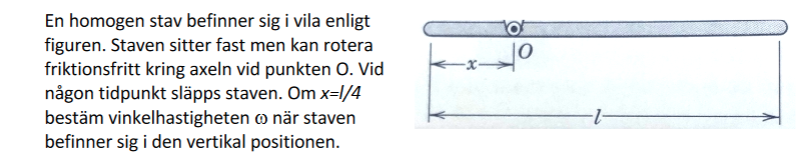Hallå, första steget att lösa denna uppgift tror jag är att ta fram tröghetsmomentet. När vi roterar runt en axel som ej är centrerad i mitten av staven så ska man nog använda sig av parallellaxelsteorem. Men en fråga först, vanligtvis så brukar det vara rotation kring z-axeln enligt denna bild.

Men i vårt fall har vi rotation kring x-axeln (om vi tänker oss xyz-planet). Gäller det fortfarande att $I=\dfrac{ML^2}{12}$ om rotationsaxeln är i mitten av staven fast med rotation kring x-axeln?

Jag har faktiskt ingen aning, blev väldigt överraskad när jag såg att vi istället roterar runt x-axeln.

Är det så att i vårat fall så har vi inget tröghetsmoment kring centrum av staven, så med parallellaxelsteoremet blir $I_o=I_{CM}+Ma^2=0+M \frac{l^2}{16}$

Svara