Trippelintegraler och Sfäriska koordinater

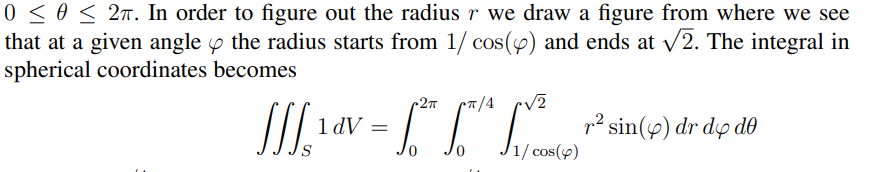
Jag tycker det ser ut som att du har ett strålknippe från origo upp till kalottytan. 

För en given stråle börjar man räkna volym när R = 1/(cos fi) och slutar när R = roten ur 2.

fi är latitudvinkeln räknat från ”nordpolen” (colatituden). Jag ska försöka rita en bild.

Ja, radien går från noll. Radien är avståndet från medelpunkten, och du vill ju ha med hela halvklotet, även de inre delarna.

Om radien går från 0.99 till 1 får du en halv pingisboll.

Bubo skrev:

Ja, radien går från noll. Radien är avståndet från medelpunkten, och du vill ju ha med hela halvklotet, även de inre delarna.

Om radien går från 0.99 till 1 får du en halv pingisboll.

Bubo, jag håller inte med. Klotet har radie roten ur 2 och skärs av ett plan som ligger 1 längdenhet från centrum. På Olivias bild ser du att det bara är biten bortom planet (från centrum) som man söker volymen för, inte för halvklotet. Hur stor del av radien som ska vara med beror av vilken vinkel strålen bildar med z-axeln.

Detta framgår av den bifogade lösningen. r går från 1/(cos fi) till roten ur 2.

Bra liknelse med strålknippen. Efter lite begrundande:

integrationelementen är ju små klossar, avhuggna strålar, med

tjocklek i r-riktningen dr

höjd fi*r

bredd theta*r *sin fi

Tokfel av mig. Jag tänkte halvklot utan att egentligen tänka.

Man kan också använda villkoret att z-koordinaten ovanför planet ska vara större än 1, dvs

$1<>$

Vi vet också att $z=R\cos(\theta)$ i sfäriska koordinater, alltså

$1<>$

Delar vi båda led med det positiva talet (övre halvplanet) $\cos(\theta)$ får vi

$\frac{1}{\cos(\theta)}<>$

Naturligtvis får R inte vara större än maximala radien $\sqrt{2}$ varvid slutligen

$\frac{1}{\cos(\theta)}<><>$

D4NIEL skrev:

Man kan också använda villkoret att z-koordinaten ovanför planet ska vara större än 1, dvs

$1<>$

Vi vet också att $z=R\cos(\theta)$ i sfäriska koordinater, alltså

$1<>$

Delar vi båda led med det positiva talet (övre halvplanet) $\cos(\theta)$ får vi

$\frac{1}{\cos(\theta)}<>$

Naturligtvis får R inte vara större än maximala radien $\sqrt{2}$ varvid slutligen

$\frac{1}{\cos(\theta)}<><>$

Fast phi istf theta.

En minor synpunkt på lösningen:

jag tycker det blir klarare om man använder r som den fria variabeln och R som konstantvärdet på skalets radie, roten(2)

Analys skrev:

En minor synpunkt på lösningen:

jag tycker det blir klarare om man använder r som den fria variabeln och R som konstantvärdet på skalets radie, roten(2)

Absolut. Jag skrev R på pappret jag plåtade, svårt att redigera i efterhand. 

Analys skrev:

En minor synpunkt på lösningen:

jag tycker det blir klarare om man använder r som den fria variabeln och R som konstantvärdet på skalets radie, roten(2)

Mm, men du får inte både ha kakan och äta den :)

D4NIEL skrev:

Man kan också använda villkoret att z-koordinaten ovanför planet ska vara större än 1, dvs

$1<>$

Vi vet också att $z=R\cos(\theta)$ i sfäriska koordinater, alltså

$1<>$

Delar vi båda led med det positiva talet (övre halvplanet) $\cos(\theta)$ får vi

$\frac{1}{\cos(\theta)}<>$

Naturligtvis får R inte vara större än maximala radien $\sqrt{2}$ varvid slutligen

$\frac{1}{\cos(\theta)}<><>$

Tack det var bra att kunna hitta värdet via kalkyleringar.

Mogens skrev:

Tack, men jag förstår inte riktigt då hur R kan bli sprt(2) om det är S i din bild som är 1/cos(fi). Då tänker jag att R blir sqrt(2)-1 om det bara är den färgade övre delen i din bild som är R. Jag förstår fortfarande inte riktigt bildligt vad R är, och hur den varierar. Nu tycker jag det ser ut som att S är 1/cod(fi) och R något annat. 

oliviav skrev:

Mogens skrev:

Tack, men jag förstår inte riktigt då hur R kan bli sprt(2) om det är S i din bild som är 1/cos(fi). Då tänker jag att R blir sqrt(2)-1 om det bara är den färgade övre delen i din bild som är R. Jag förstår fortfarande inte riktigt bildligt vad R är, och hur den varierar. Nu tycker jag det ser ut som att S är 1/cod(fi) och R något annat. 

Jag gjorde två bilder igen.

På den vänstra bilden om det är så att om R minskar så blir det som att det varit ett mindre klot och volymen minskat? (Grön större R, men konstant runt hela det klotet) och (Rosa mindre R, och nu blir volymen mindre av klotet pga R minskat)

Den högra bilden, som i uppgiften vi pratar om, undrar jag om R börjar i origo som i den rosa R och att fi blir "som vanligt"? Det är väl fel att tänka att R blir som i den turkosa R och då får ett annat fi?

Tack för hjälpen!

Jag var slarvig. Beteckningen R i min figur är inte bra.

Tänk så här. Du har en apelsin med radie roten ur 2. Med ett rakbladsvasst svärd gör vi ett rakt snitt vinkelrätt mot z-axeln som tar av en kalott (segment heter det kanske). Där snittet träffar z-axeln är avståndet till apelsinens centrum 1.  

Vi vill veta volymen av segmentet. Då tänker vi oss ett strålknippe ut från origo till klotytan. Betrakta en stråle med vinkeln fi från z-axeln. Den träffar snittytan på avståndet 1/ cos fi från origo (se min fig). Så när vi integrerar med avseende på r så är undre gränsen 1/cos fi och övre gränsen roten ur 2.

Ju större fi desto kortare väg genom segmentet. När 1/cos fi = roten ur 2 så slutar vi

(dvs när fi = pi/4). 

Theta är longitudvinkel, den går ett varv runt österut från 0 till 2pi.

Fi är (co)latitud, den går från nordpolen ner till Bordeaux ungefär, från 0 till pi/4.

r går från 1/cos fi till roten ur två.

Tag fram en apelsin och en rejäl kökskniv så ser du hur det funkar.

Mogens skrev:

Jag var slarvig. Beteckningen R i min figur är inte bra.

 

Tänk så här. Du har en apelsin med radie roten ur 2. Med ett rakbladsvasst svärd gör vi ett rakt snitt vinkelrätt mot z-axeln som tar av en kalott (segment heter det kanske). Där snittet träffar z-axeln är avståndet till apelsinens centrum 1.  

Vi vill veta volymen av segmentet. Då tänker vi oss ett strålknippe ut från origo till klotytan. Betrakta en stråle med vinkeln fi från z-axeln. Den träffar snittytan på avståndet 1/ cos fi från origo (se min fig). Så när vi integrerar med avseende på r så är undre gränsen 1/cos fi och övre gränsen roten ur 2.

Ju större fi desto kortare väg genom segmentet. När 1/cos fi = roten ur 2 så slutar vi

(dvs när fi = pi/4). 

Theta är longitudvinkel, den går ett varv runt österut från 0 till 2pi.

Fi är (co)latitud, den går från nordpolen ner till Bordeaux ungefär, från 0 till pi/4.

r går från 1/cos fi till roten ur två.

Tag fram en apelsin och en rejäl kökskniv så ser du hur det funkar.

Jaaa, tack så mycket! Nu fattar jag bildligt hur det funkar!