Trippelintegral, bestämma gränser

Hej!

Jag försöker lösa denna uppgift: "Beskriv den kropp som begränsas av cylindern $x^2+z^2=a^2$ samt tre plan y=0, z=0 och y=x. Beräkna dess volym."

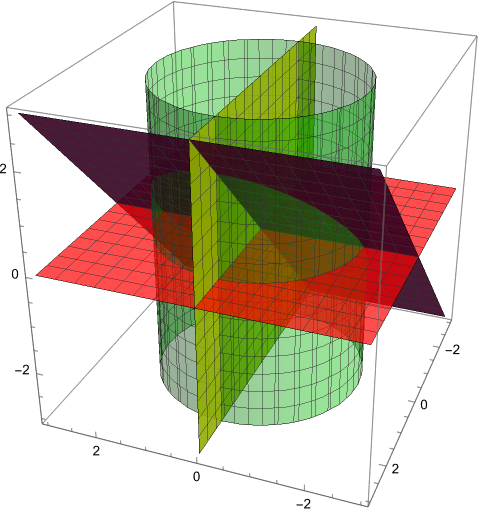
Jag har försökt rita upp området och får fyra st identiska "osymmetriska tårtbitar" som ligger lite olika orienterade men med samma volym, tänker därför att det räcker att jag beräknar volymen av en tårtbit och sedan tar x4. Här kommer en bild på området:

Jag har trixat ett bra tag med gränserna nu, men för alla mina försök blir volymen =0, vilket känns fel. I mitt senaste test satte jag: $0\le z\le \sqrt{a^2-x^2}$, $0\le y\le x$ och $0\le x\le a$, vilket alltså inte funkade. Jag blir lite förvirrad av att den "båge" som går i y=x-planet från origo till punkten (a,a,0) ju inte är en fjärdedels cirkel utan snarare en fjärdedels oval eller nåt. Hur får jag in det i min gränsdragning?

Tacksam för tips!