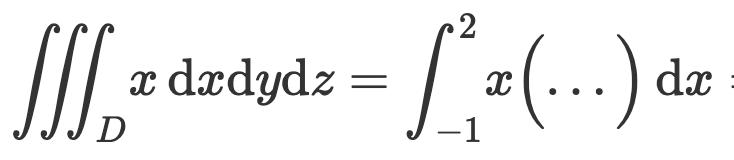Trippelintegral
Fråga:
 Området:
Området:

Min lösning:

Någon som kan ge tips på hur man ska tänka? Tror inte man skall använda sig av sfäriska koordinater men kommer inte på något annat sätt. Tror mina gränser är inkorrekta också, hjälp uppskattas !!
Försök tänk efter vad det är för en kropp och hur du kan dela upp trippelintegralen i "nivåer". Du kommer att finna ett enkelt samband i yz-planet.
tänkte -1<x<2, -sqrt(9-z^2)<y<sqrt(9-z^2), -1<z<1 men det stämmer ej, skulle du kunna ge någon med ledning?
Kommer du vidare på nedan?

Fundera sedan på vad ... är
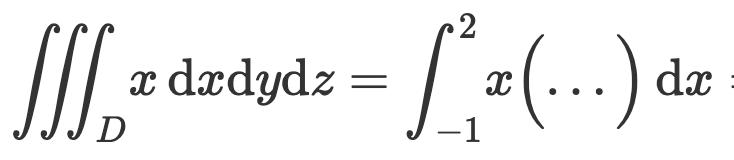
Kan du skriva ... som en dubbelintegral, och vad representerar denna?
Hänger med på det du skickat men förstår inte riktigt hur jag ska ta mig vidare från sista steget
Vad skall stå inom (…)?
Trinity2 skrev:Kommer du vidare på nedan?
Fundera sedan på vad ... är
Kan du skriva ... som en dubbelintegral, och vad representerar denna?
Får intervallet:

Tänker direkt på polära koordinater men vet inte riktigt hur jag ska tänka när det det är y och z istället för x och y
Räknat om och får detta nu, vilket jag tycker känns bra, men i facit står det 7pi/4, antar att jag fortfarande missar något

Det här är bra
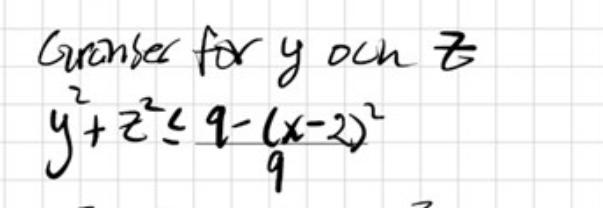
tänk nu bara i yz-planet och låt x vara fixt. Vad beskrivs med denna formel i yz-planet?
Borde vara en cirkelskiva i yz-planet och vara en cylinder om man inkluderar x variabeln?
Iggelopiggelo skrev:Borde vara en cirkelskiva i yz-planet och vara en cylinder om man inkluderar x variabeln?
Fokusera på den första biten i ditt påstående. Hur stor är radien på denna cirkelskiva?
Radien är 1
Iggelopiggelo skrev:Radien är 1
Nej, för y^2+z^2≤1 är radien 1, men inte i ditt fall.
Vilken radie har
y^2+z^2≤25 ?
y^2+z^2≤9 ?
y^2+z^2≤16 ?
5,3,4.
så i detta fall sqrt(1-((x-2)/3)^2)
Iggelopiggelo skrev:5,3,4.
så i detta fall sqrt(1-((x-2)/3)^2)
Det första är rätt, och det sista också, nästan...
Var är roten ur högerledet i
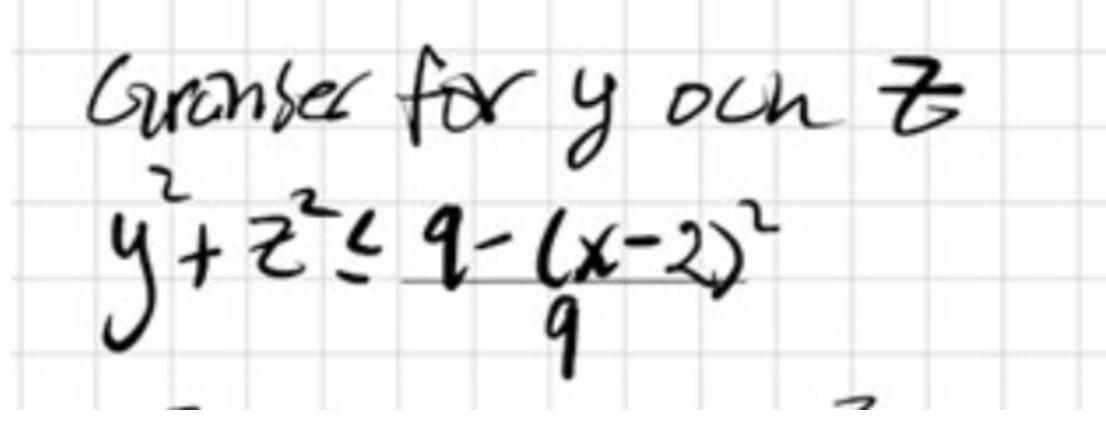
(Det kan förenklas _lite_, men inte så mycket)
Ser inte hur det kan förenklas ytterligare från det jag skrev, är såklart +- men negativa förkastas eftersom en radie ej kan vara negativ
Titta på #4 igen
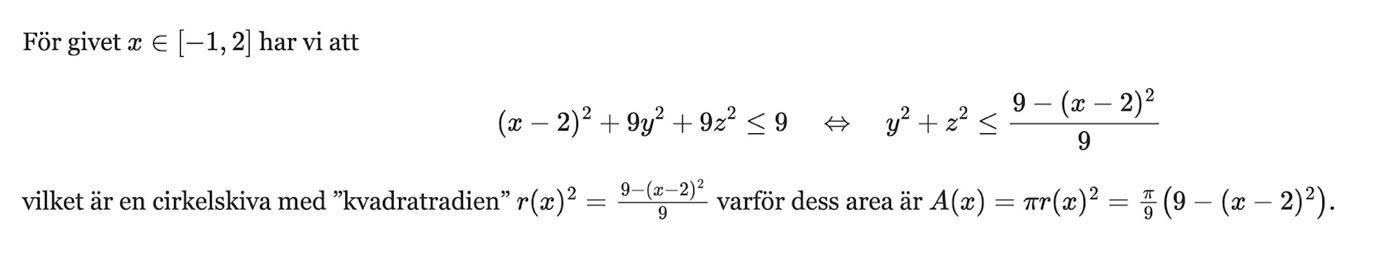 är du med på detta?
är du med på detta?