Trippelintegral
Hej!
Jag har fått för mig att man brukar beräkna trippelintegraler över volymer, men i uppgiften nedan tolkar jag T som en yta. Sen skriver facit att T är området i första kvadranten? Skriver de så för att det är det man menar när man skriver trippelintegralen över en yta?
En följdfråga: hade det varit fel att dela upp ytan i T1 och T2 som jag gjort nedan? Det ger samma svar som facit :)


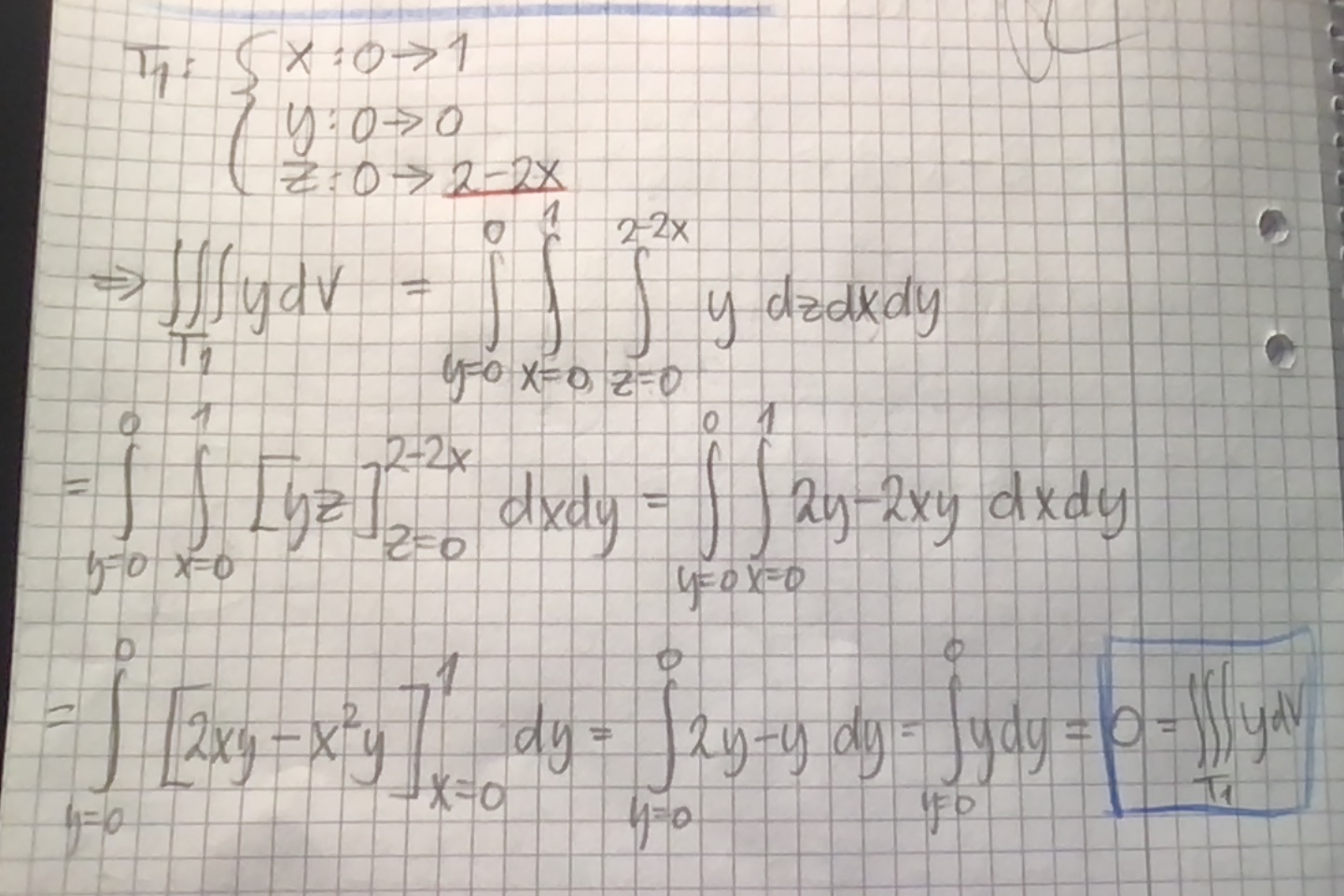

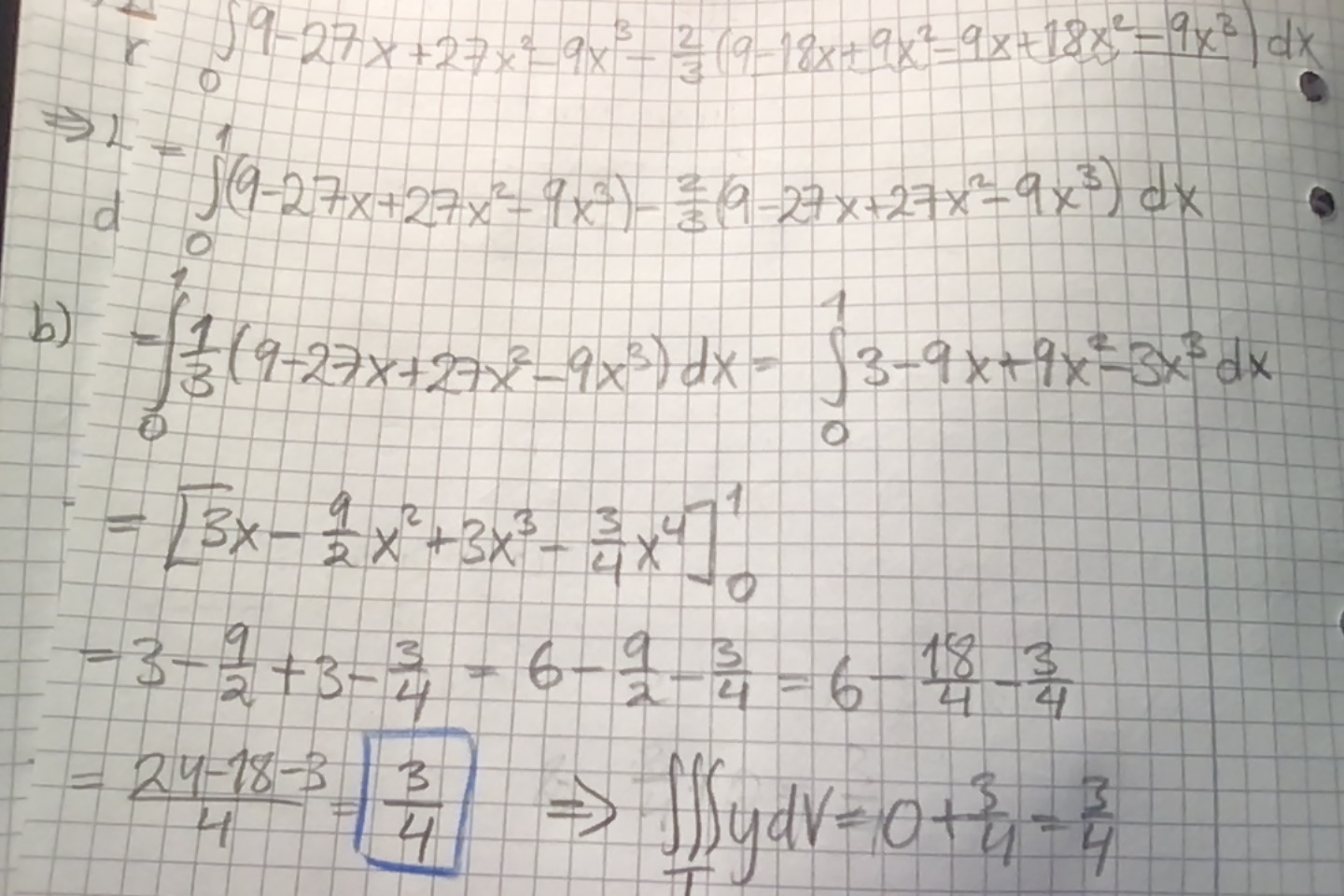
Nejdå, T är en volym.
Man integrerar funktionen från "botten" (dvs z=0) upp till z-värdet (2-2x-2y/3) över hela det tvådimensionella intervallet D som är "basytan" i T.
Den funktion man integrerar är f(x,y,z) = y.
Tack för svaret Bubo! Så även om de bara anger 4 hörn, ska jag tolka det som att det är en volym så länge det är en trippelinegral, och att de andra sidorna då utgörs av de positiva xy- respektive yz-planen?
Fyra punkter som inte ligger i samma plan definierar ju en tetraeder.
Det är självklart: Tre punkter ger oss alltid ett plan, och om den fjärde punkten inte ligger i det planet så kommer den att ge oss en tetraeder (pyramid). Jämför med hur en trebent pall alltid står bra på ett golv. En fyrbent stol står bara bra om alla fyra benen rör marken samtidigt (ligger i samma plan). Om det fjärde benet är för långt eller för kort får vi "en pyramid".
Jaaa nu förstår jag, tack Bubo!


