trigonometriska modeller ex. uppgift
hej! jag går genom förklaringen av en exempel uppgift i matte boken men förstår inte riktigt sista steget. 
Jag förstår hur man räknar fram värdet på A, k och d men jag fastnar på t och v delen. Så här står det i boken angående dessa: 
jag förstår att de sätter högsta höjden (dvs startvärdet) lika med hela funktionen och att tiden då är 0s eftersom punkten vi undersöker befinner sig där vid t=0, men från och med raden sin(pi/25 v) = 1 är jag helt lost.
Jag vet att v-värdet representerar förskjutningen i x-axeln om man kollar på en graf, men jag förstår inte riktigt hur jag ska använda mig av det här när jag har istället ritat en cirkel som de gjorde i förklaringen (infogar bild på cirkeln från förklaringen nedan)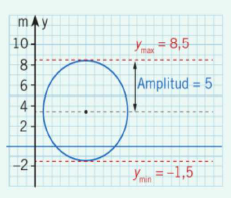 
uppskattar all hjälp! :)
seedra2004 skrev:[...]
, men från och med raden sin(pi/25 v) = 1 är jag helt lost.
[...]
Vi har ekvationen
Vi förenklar en smula genom att tillfälligt byta ut mot .
Vi får då ekvationen
Med hjälp av enhetscirkeln ser vi att denna ekvation har lösningarna
Nu byter vi tillbaka från till , vilket ger oss
Vi löser ut genom att multiplicera båda sidor med :
Alla dessa värden på ger det önskade resultatet. Vi väljer det enklaste, nämligen .
Blev det tydligare då?
Yngve skrev:seedra2004 skrev:[...]
, men från och med raden sin(pi/25 v) = 1 är jag helt lost.
[...]Vi har ekvationen
Vi förenklar en smula genom att tillfälligt byta ut mot .
Vi får då ekvationen
jaha alltså sätter vi att sin(w) är lika med 1 eftersom punkten vi undersöker i detta fall anger den högsta möjliga värdet på y och därmed antar själva sinusfunktionen det största värdet den kan anta, dvs 1?
Ja, eller egentligen att det står att vi ska utgå från den punkt som.är högst upp då t = 0.
Högst upp är 8,5 meter ovanför vattenytan, vilket ger oss att y = 8,5 då t = 0.
