Trigonometriska ekvationer med sinus

hur löser man sin (3x) = sin(x)? Läroboken jag läser står det att dem använder formel " $\cos b = \cos a \Leftrightarrow b = \pm a + k 2 π$ "

Jag får då följande x-värdena: $x_{1} = πk$ och $x_{2} = \frac{π}{2} k$

men i facit står det att lösningen är $x = πk eller x = \frac{π}{4} + k \frac{π}{2}$ .

Flyttad till matematik 3 - trigonometri från matematik - universitet /Dracaena

Du (eller möjligen boken) verkar blanda ihop sinus och cosinus. Rita upp enhetscirkeln!

sin(3x) = sin(x)

$3x=x+2\pi n$ eller $3x=\pi-x+2\pi n$

Kommer du vidare?

så helt enkelt, formeln $\cos b = \cos a \Leftrightarrow b = \pm a + k 2 π$ gäller bara för cosinus, men för sinus så gäller det att istället för $\pm a$ så är det $π - a eller a$ ???

Ja. Rita upp enhetscirkeln!

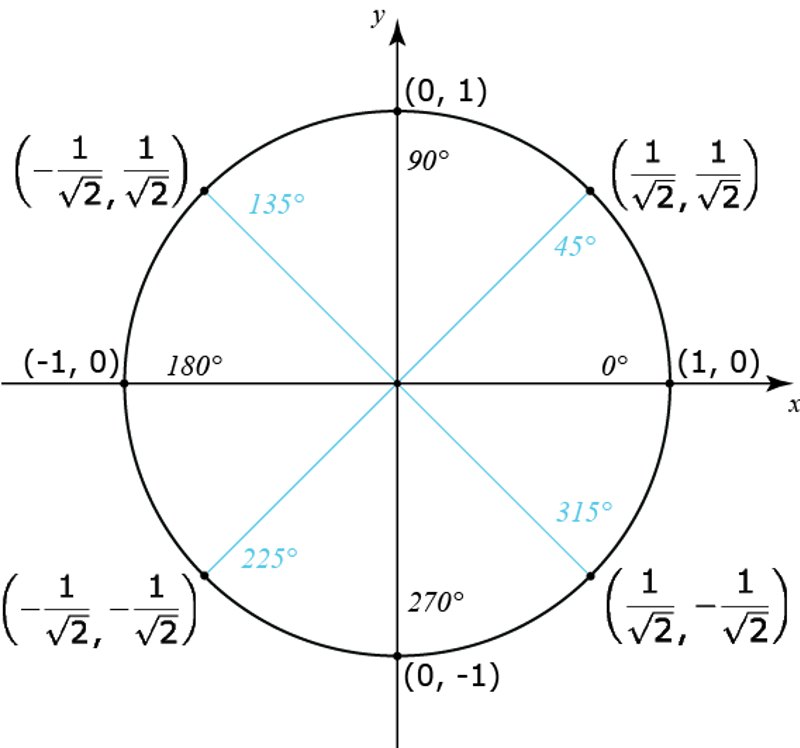
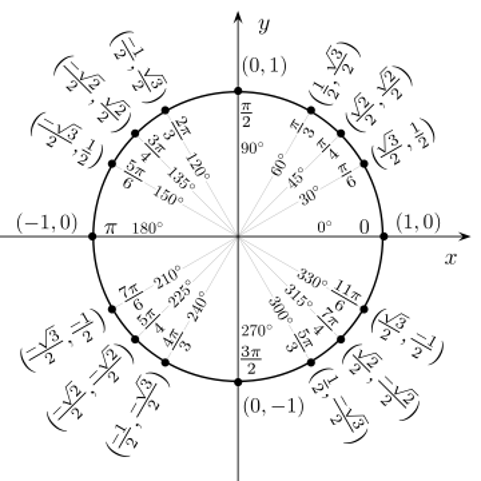
Tack så mycket! Nu fattar jag!

Svara

Visa senaste svar