Trigonometriska ekvationer
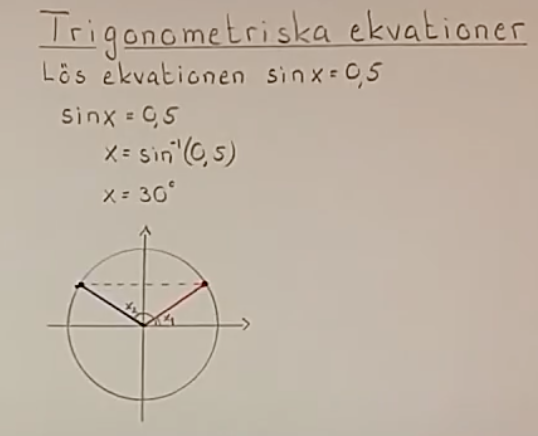
hur kan sinx=0,5 bli -> x = sin^-1(0,5)
vad är det för regel?
Hej.
Lite slarvigt så kan vi säga att sin-1(0,5) är ett sätt att skriva den inversa "funktionen" till sinus. Det är ett olyckligt val av nomenklatur eftersom sin-1(0,5) kan misstolkas som 1/sin(0,5).
Det är lite liknande att den inversa "funktionen" till är .
Ett problem är att eftersom sinusfunkionen är periodisk så finns det inte endast en vinkel x som uppfyller att sin(x) = 0,5.
I själva verket finns det oändligt många sådana vinklar.
För att hantera det på ett bra sätt brukar man använda "arcus"-funktioner, därbåde definitionsmängd och värdemängd är begränsade.
I det här fallet arcsin, som har en definitionsmängd som är [-1, 1] och en värdemängd som är [-90°, 90°].
Vi skriver då så här:
sin(x) = 0,5 innebär att
- x = arcsin(0,5) + n•360°
- x = 180° - arcsin(0,5) + n•360°
Här har vi att arcsin(0,5) = 30°
Yngve skrev:Hej.
Lite slarvigt så kan vi säga att sin-1(0,5) är ett sätt att skriva den inversa "funktionen" till sinus. Det är ett olyckligt val av nomenklatur eftersom sin-1(0,5) kan misstolkas som 1/sin(0,5).
Det är lite liknande att den inversa "funktionen" till är .
Ett problem är att eftersom sinusfunkionen är periodisk så finns det inte endast en vinkel x som uppfyller att sin(x) = 0,5.
I själva verket finns det oändligt många sådana vinklar.
För att hantera det på ett bra sätt brukar man använda "arcus"-funktioner, därbåde definitionsmängd och värdemängd är begränsade.
I det här fallet arcsin, som har en definitionsmängd som är [-1, 1] och en värdemängd som är [-90°, 90°].
Vi skriver då så här:
sin(x) = 0,5 innebär att
- x = arcsin(0,5) + n•360°
- x = 180° - arcsin(0,5) + n•360°
Här har vi att arcsin(0,5) = 30°
Superstort tack!!


