Trigonometrisk ekvation

eddberlu skrev:

Heej! Jag undrar vad x faktiskt är här. Vad är det man räknar ut menar jag. Har sett att i genomgången är svaret Sin x = 0.66.

Jag tror inte riktigt jag förstår vad Sin x faktiskt betyder. Innebär det vinkeln av x-värdet?

samt hur vet man att det bli cos i uppgift b? 

Uppgiften är felformulerad..

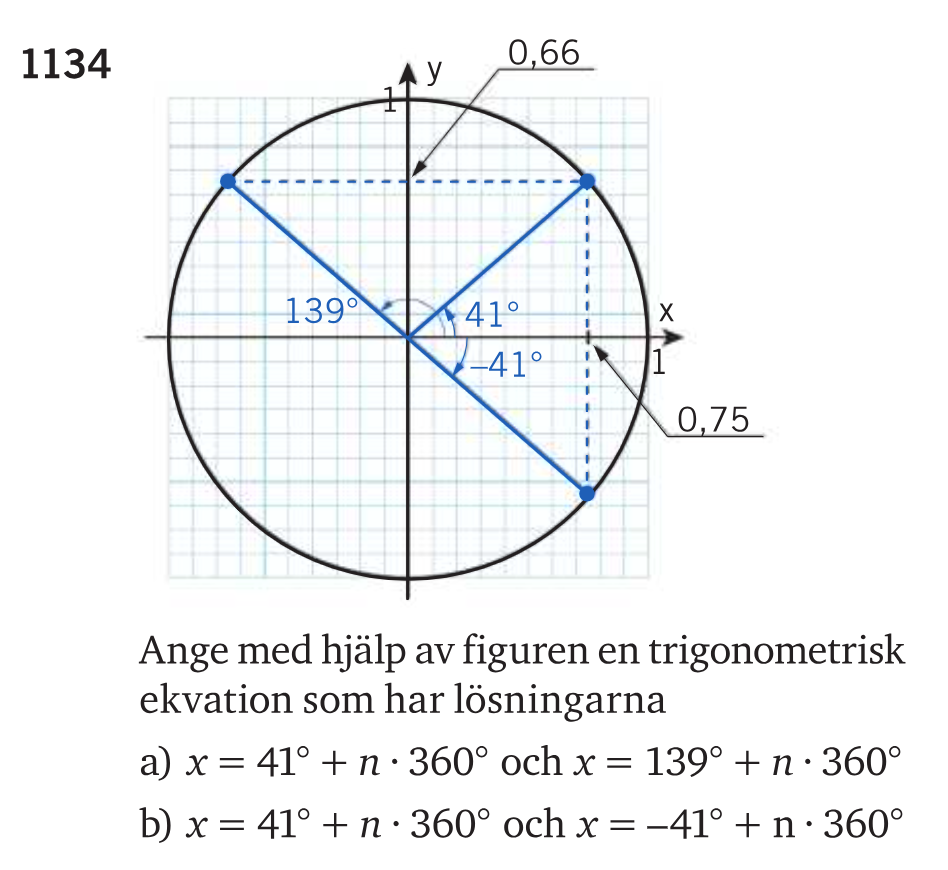
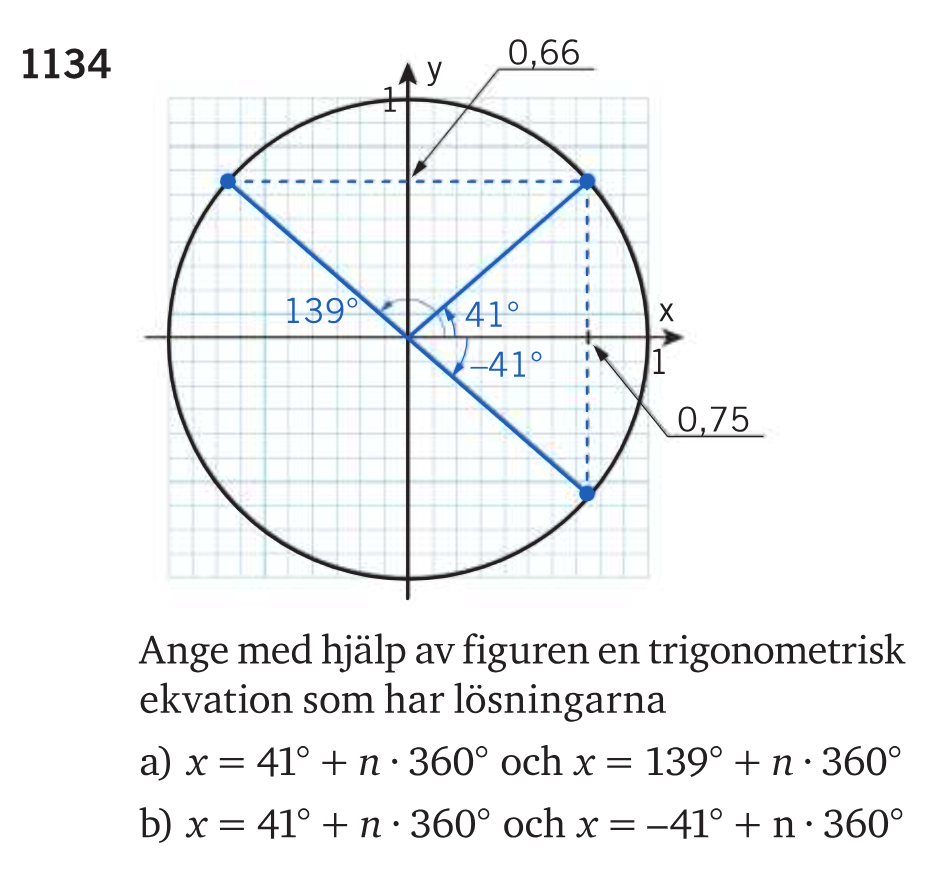
De använder symbolen x både för att ange en horisontell koordinat och för att ange en vinkel. Detta är fel.

Om vi istället kallar vinkeln för v så hänger allt ihop. Då gäller nämligen för alla punkter (x, y) på enhetscirkeln att

• x = cos(v)
• y = sin(v)

Med hjälp av enhetscirkeln kan vi då se att

• cos(41°) = 0,75 eftersom x-koordinaten för punkt A är 0,75.
• cos(-41°) = 0,75 eftersom x-koordinaten för punkt C är 0,75.
• sin(41°) = 0,66 eftersom y-koordinaten för punkt A är 0,66.
• cos(139°) = 0,66 eftersom y-koordinaten för punkt B är 0,66..

Var det svar på din fråga?

Yngve skrev:

Uppgiften är felformulerad..

De använder symbolen x både för att ange en horisontell koordinat och för att ange en vinkel. Detta är fel.

Om vi istället kallar vinkeln för v så hänger allt ihop. Då gäller nämligen för alla punkter (x, y) på enhetscirkeln att

• x = cos(v)
• y = sin(v)

Med hjälp av enhetscirkeln kan vi då se att

• cos(41°) = 0,75 eftersom x-koordinaten för punkt A är 0,75.
• cos(-41°) = 0,75 eftersom x-koordinaten för punkt C är 0,75.
• sin(41°) = 0,66 eftersom y-koordinaten för punkt A är 0,66.
• cos(139°) = 0,66 eftersom y-koordinaten för punkt B är 0,66..

Var det svar på din fråga?

Det var strålande svar på min fråga!! Tack!! En följdfråga, hur skulle man ex förklara "cos(139°) = 0,66 eftersom y-koordinaten för punkt B är 0,66.." i text? Ledsen att det blir luddigt här men undrar alltså exakt vad cos är. Är cos(139) att säga att när vinkeln är 139 grader så är x kordinaten ... osv


Tack igen!! 

Bästa,

E

En följdfråga, hur skulle man ex förklara "cos(139°) = 0,66 eftersom y-koordinaten för punkt B är 0,66.." i text? Ledsen att det blir luddigt här men undrar alltså exakt vad cos är. Är cos(139) att säga att när vinkeln är 139 grader så är x kordinaten ... osv

Nej, om du tittar på bilden så ser du att vinkeln 139^o ligger i andra kvadranetn, d v s x-värdet är negativt så cos(139^o) = -0,66, d v s lika stort som för 41^o men negativt..

Tillägg: 24 nov 2023 13:53

Oj, jag rörde ihop sinus och cosinus... Värdet var sinus men resonemanget var cosinus (hoppas jag skrev rätt nu...)

eddberlu skrev:

Det var strålande svar på min fråga!! Tack!!

Vad bra! Varsågod 😀

En följdfråga, hur skulle man ex förklara "cos(139°) = 0,66 eftersom y-koordinaten för punkt B är 0,66.." i text?

Det är sinusvördet som.är 0,66 inte cosinusvärdet.

Det kan beskrivas så här:

• Rita en enhetscirkel i ett x/y-koordinatsystem.
• Rita en radie i denna cirkel så att motursvinkeln från den positiva delen av x-axeln är v.
• Markera en punkt A där radien möter enhetscirkeln.
• Punkten A har nu koordinaterna (cos(v), sin(v))

undrar alltså exakt vad cos är. Är cos(139) att säga att när vinkeln är 139 grader så är x kordinaten ... osv

Se ovan.

Smaragdalena skrev:

[...]

cos(139^o) = -0,66

[...]

Typo, det ska stå cos(139°) = -0,75.

(Det går inte att skicka PM till dig Smaragdalena.)