Trigonometri

Fråga lyder följande:

Du har en triangel ACB

Motstående sida av B är 10cm

Motstående sida av A är 6cm

Det vi kallar basen eller motstående av C är okänd.

Bestäm ett c så att A = 30 grader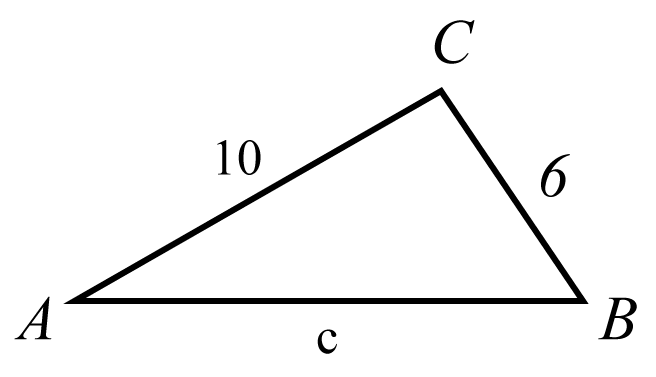

Resonera kring om man skulle kunna använda både cossinussatsen och sinussatsen eller om bara en skulle vara bäst.

Avrunda till två decimaler.

 

Mitt svar:

Jag försökte först att lösa frågan med Sinussatsen, eftersom att jag såg att man kunda dela sin30/6 = sinB/10 för att få vinkeln B

Jag fick vinkeln B till att bli 56,44 grader

Nu tog jag reda på vinkeln C med vinklarna A=30 med B=56,44. 180-30-56,44 = 93,56

C=93,56

Nu kunde jag ta reda på ett av fallen med sinussatsen: c/sin93,56 = 6/sin30 

Då blir c(1) = 11,98

Jag vet inte hur jag skall kunna få det andra fallet med sinussatsen så jag svara med att det inte GÅR att få ett till fall med SINUSSATSEN. (Sinussatsen med två fall)

 

Jag försöker nu att lösa problemet med cossinussatsen.

6^2=c^2+10^2-2 x c x 10 x cos30

=>

36 =c^2 + 100 - 20c x cos30

=>

c^2+64-10sqrt3xc=0

=>

c^2+64-17,32c = 0

PQ-Formel

8,66(+-)sqrt74,9956-64

=>

8,66(+-)sqrt10,9956

=>

8,66(+-)3,32

=>

c(1)=11,98

c(2)=5.34

 

 

Mitt resonemang är att man inte kan använda sinussatsen vid två fall vid det här tillfället. Det bästa alternativet var att använda cossinussatsen då vi fick två möjliga svar på c som kunde ge vinkeln 30 grader på A.

 

Anledningen till att jag publicerar är att jag inte är säker om man kan få två fall eller inte med sinussatsen som ger samma svar som med dem på cossinussatsen.