Om jag säger att energin bevaras, vad säger du då?
jag säger inget för det stämmer
Kan du utnyttja det faktum att energin bevaras? Alltså ställa upp en ekvation?
ja typ 0,67-x
Det är ett uttryck, inte en ekvation. Vad står x för i detta fall?
x står för linjen, om du kollar på ritningen jag gjort
Ah, sorry jag såg inte den först!
Vad får du (i ord) om du tar 0,67-x?
då får jag den biten under linjen
Ja! Ska vi kalla den biten något? Förslagsvis h? Hur kan vi få ett värde på h?
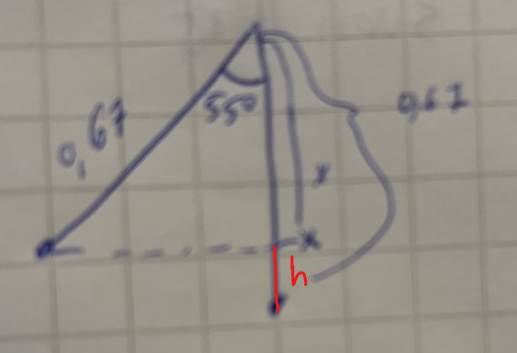
genom att ta cosinus eller sinus eller? och ta reda på x först genom det. Sedan tar man 0.67-x för att ta reda på H. Problemet är att jag blandar ihop cosinus med sinus och det
Det är en bra idé. Du väljer: sinus eller cosinus!
Va, hur då?
Vet du "uttrycken" för sin(v) respektive cos(v) i ord? Ta hjälp av dess ord:
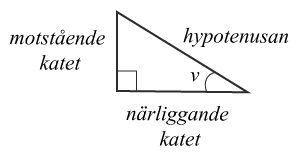
nej, jag har glömt. men sin ska va motstående/hypotenusan och cos ska va närliggande delat på hypotenusan
Ja. Nu har vi vinkeln 55 grader. Är det den motstående eller närliggande sidan som vi vill räkna ut?
närliggande alltså cos
Jippi! Kan du nu teckna ett uttryck för vinkeln genom att använda cosinus?
x/0.67? cos(55grader)
Om ? är ett =, ja! Beräkna nu x och sedan h.
omg tack sååå mycket! Har haft problem med det men nu lärde jag mig det på knappt 5 min
Kommer du vidare och kan lösa hela uppgiften då?
Nope, varför ska jag beräkna h?
Det är här vi ska utnyttja att energin bevaras. I ursprungsläget har kulan lägesenergi, men ingen rörelseenergi (vi släpper den från stillastående). Vad har kulan för sorters energi i det understa läget?
Rörelseenergi
Precis. Hur tecknas lägesenergi? Hur tecknas rörelseenergi?
mgh för läges och mv^2/2 för rörelse
Grymt! Kan du då ställa upp en ekvation som säger att energin bevaras?
ja vänta
Jajamen. Var noga med att roten ur-tecknet går hela vägen över h också! Lyckas du lösa den?
blir höjden h?
Ja vad blir höjden egentligen? Skillnaden i höjdled mellan kulans startläge och det understa läget.
Nu kanske du själv kan besvara din fråga i inlägg #23?
Ja, då stämmer det.0.0964meter
det blir alltså 1.3 meter/sekund. Men hur blir det längre? Jag har fått sveret men förstår inte riktigt än. Eller jo jag kanske förstår. Att man först tar 0.67+ h för lägesenergin och sedan tar minus 0.67 för att räkna höjden i skillnad. Eller mg(h0-h1) Tänker jag rätt nu?
Jag får inte samma värde som du. Vad får du för värde på x?
Går det lättare att tänka om du sätter höjden i kulans nedersta läge som 0 m?
Jag får värdet 0.5735, mitt svar stämmer ihop med facit. Det är nog du som har slarvat
Led mig genom din beräkning! Om det är enklare kan du ladda upp en bild på din uträkning, inklusive alla siffror.
okej vänta
Ta hjälp av inlägg #19 och #20. Du har nu endast beräknat cos(55). Detta är inte samma som x.
fast, jag fick samma svar som facit. var tänker du att jag har gjort fel
Då verkar facit sorgligt nog ha fel i detta fall :( . Förhoppningsvis kan vi själva få rätt svar om vi tar det steg för steg.
I inlägg #19 (och med stöd av inlägg #20 där jag ber dig byta "?" mot "=") skrev du en ekvation för x. Där står det inte att x = cos(55). Vad står det?
haha, ja du har rätt.
Hur blir det då? Uträkningen och värdet för x.
x/0.67=0.57 då blir x 0.38
Ja! Vad behöver vi göra härnäst?
0.67-0.38 =0.28, vilket är h
Jag får det till 0.29 om jag avrundar till två värdesiffror.
okej. jag ersätter nu
då får jag harstigheten till 2.38m/s
Det verkar som att du avrundar lite vid varje beräkning. Mitt svar är 2.368... m/s och då har jag inte avrundat i något steg.
Men, i denna upgift och i en annan får jag som svaret där uppe 1.3m/s. Varför har facit ett sådant svar?
Troligtvis för att facit precis som du glömde att multiplicera med 0.67. Varför läroboksförfattarna missade detta är dock ett mysterium.
Efter lite googlande hittade jag samma uppgift, fast med rätt svar:

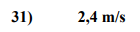
Jaaa då har du rätt! Tack så hemskt mycket!
Nu är jag nöjd med svaren! Tack för att du finns:) annars hade jag gett upp


 Hur ska jag tänka här?
Hur ska jag tänka här?


