Trevlig ma3 uppgift
Hej Pluggakuten! Jag har en extremt trevlig ma3-uppgift jag skulle vilja dela med er:
I ett koordinatsystem finns två kurvor inritade:
f(x)=1-x för alla x>0 och y(x)=1-x² för alla x<0. En rektangel ritas in i koordinatsystemet. Ett av hörnen ligger på f(x), ett av hörnen ligger på y(x), och de resterande två ligger på x-axeln. Bestäm rektangelns maximala area.
Då det är en ma3-uppgift får man inte använda kedjeregeln! ;)
Man tittar bara på y(x) > 0 och f(x) > 0, antar jag?
Ja, precis. Ingen punkt ligger under x-axeln.
Jag tycker inte jag behöver någon kedjeregel. Har jag gjort fel?
Posta din lösning så får vi se! Jag ska bistå med mitt lösningsförslag inom kort.
Jag skriver bara mitt svar, som ser rätt kul ut: .
Lösningsförslag
Låt oss börja med att skissa hur rektangeln skulle kunna se ut:
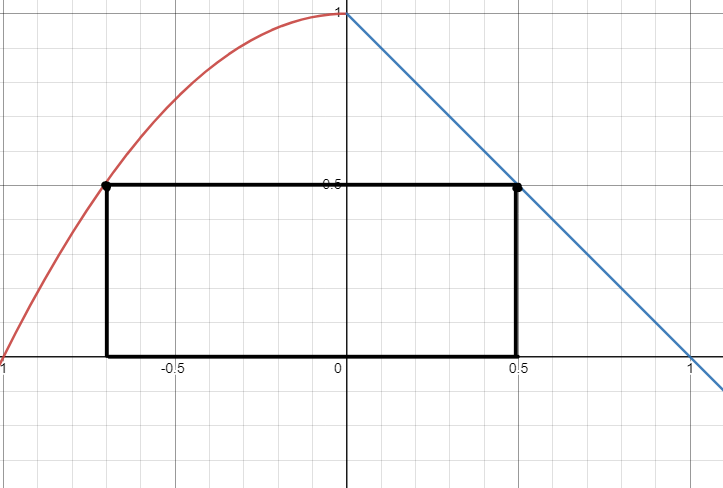
Det vi kan kostatera är att rektangeln kommer ha en bas som består av differensen av x-koordinaten till höger om y-axeln och x-koordinaten till vänster om y-axeln. Höjderna kommer vara respektive .
Vi kan namnge dessa länger i figuren:
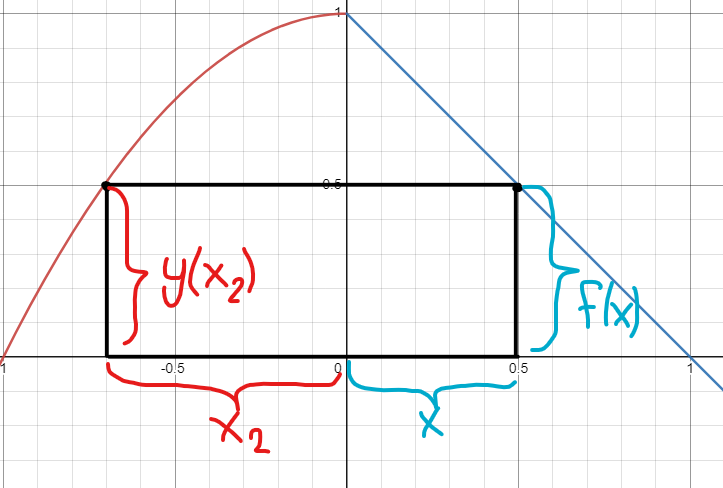
Eftersom rektangelns höjd måste vara lika på båda sidor om y-axeln vet vi att:
Vi kan utesluta roten eftersom vi vet att koordinaten .
Ur detta kan vi skapa en funktion för arean:
Vi ser ur vår figur att .
Nu gäller det att hitta extrempunkterna till areafunktionen. Detta gör vi lättast genom att derivera och sätta :
Denna tredjegradare kan verka läskig men allt vi behöver är lite röta! Om man testar några rötter ser man direkt att är en rot. Med polynomdivision kan vi sedan skriva om ekvationen till: .
Sedan använder vi valfri metod för att skriva om andragradspolynomet på nollställesform och får då:
Nu har vi alltså lösningarna till ekvationen :
kan vi direkt utesluta som potentiell extrempunktskandidat eftersom ligger utanför definitionsmängden. Då gäller det att ta fram och testa vilken av och som är maximipunkten:
Vi ser att , varför är maximipunkten.
Nu stoppar vi in i vår funktion och får då:
Märk väl att jag kan ha gjort räknefel någonstans, det finns inget facit. Skriv därför gärna ut hela era uträkningar.
Tillägg: 2 mar 2023 18:12
Jag hittade just ett litet fel. Min ekvationslösning är felaktig, men svaret blev rätt ändå! Ha det i åtänkte om ni läser lösningsförslaget.
Laguna skrev:Jag skriver bara mitt svar, som ser rätt kul ut: .
Jag får ett svar som är större. Hur ser din areafunktion ut?
Jag gjorde fel. Nu får jag samma area som du. Jag utgick från den vänstra hörnpunkten x = -a. Då slapp jag kvadratrötter. Arean = (a+a2)(1-a2).
Det kan man skriva om som a(1+a)(1-a2) = a(1+a)(1-a)(1+a) = a(1-a)(1+a)2.
(1+a)2 = 1+2a+a2 och dess derivata är 2+2a = 2(1+a). Derivering med produktregeln av arean ger A' = 2(a-a2)(1+a) + (1-2a)(1+a)2.
A' = 0 har en lösning 1+a = 0, den kan vi dividera bort så har vi 2(a-a2)+(1-2a)(1+a) = 0. Och sen löser man det.
Ah, trevligt. Betydligt mindre krånglig än min lösning! Snyggt!



