Transfer function
Hej! Jag ska härleda överföringsfunktionen för schemat nedan med hjälp av komplexa impedans metoden.
För de parallella komponenterna kom jag fram till:
Z1,2=Z1·Z2Z1+Z2=Ls·R
Sedan får jag till
Är det rätt?
Schemat
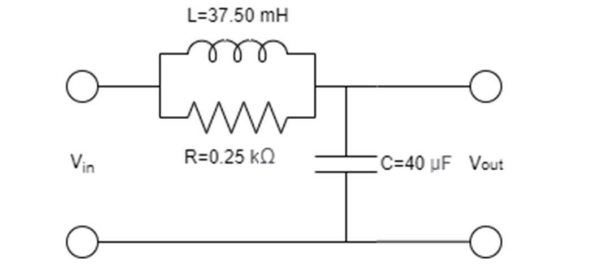
H(s) brukar definieras som utsignal dividerad med insignal och då är det Z3/(Z1,2+Z3).
Håller med Jan Ragnar.
Sen är det nog ett fel i sista ledet där det nedersta Cs har försvunnit. Kolla det när du räknar om.
Om man ska använda komplexa metoder, ska man inte då använda jw i stället för s?
Kom fram till det här nu:
Om man ska använda komplexa metoder, ska man inte då använda jw i stället för s?
Jag ska använda Matlab sen, så jag kommer nog byta till då.
Ser OK ut, tycker jag.
Ok!
Nu står det: "Derive an analytical expression for the step response of your filter in time domain."
Jag kom fram till 
Ska jag nu bryta ut en faktor på för att kunna hitta inversen till Laplacetransformen?
Bump
Du verkar ha med en faktor för mycket av Cs i nämnaren till Y(s).
Nästa steg bör vara att föra in numeriska värden på R, L och C och sedan partialuppdela bråkuttrycket i s innan övergång till tidsdomänen.
Jan Ragnar skrev:Du verkar ha med en faktor för mycket av Cs i nämnaren till Y(s).
Men då måste mitt vara fel?
Jag tycker H(s) = (Ls+R)/(RLCs2+Ls+R).
Jan Ragnar skrev:Jag tycker H(s) = (Ls+R)/(RLCs2+Ls+R).
Jag håller med dig nu. Jag skrev bara fel i uttrycket för . faktorerna stryker bort varandra!

Jag har nu kommit fram till det här:

Nästa steg är att jag ska partiellbråksuppdela för att sedan hitta , men jag har får inte till det!
bump :(
Jag måste erkänna att mina eventuella kunskaper om Laplacetransform har eroderat betänkligt med åren. Inte ens en titt i min gamla lärobok från 1983 gav någon aha-upplevelse.
Jag är nog mer vilsen än du är, är jag rädd.
ThomasN skrev:Jag måste erkänna att mina eventuella kunskaper om Laplacetransform har eroderat betänkligt med åren. Inte ens en titt i min gamla lärobok från 1983 gav någon aha-upplevelse.
Jag är nog mer vilsen än du är, är jag rädd.
XD, det är inte så ofta man håller på med transformer kanske!
Nä men, jag vet vad jag ska göra, men får inte till det! Jag ska (?) partiellbråksuppdela för att sedan kunna hitta inversen, dvs, . Jag har själv räknat på det många gånger, men jag ser inte hur jag kan komma vidare här!
Har du svaret på uppgiften?
Jan Ragnar skrev:Har du svaret på uppgiften?
Nej:)
Jag måste ha tänkt lite fel.
Bör väl vara 1 - e-50t(…….)
Borde inte den grönmarkerade termen vara om du bryter ut ett ?
i nämnaren har vi
Så tänker jag:

Ja, du har helt rätt. Jag har vänt R och L fel. Du får räkna om med rätt faktor i täljaren. Förhoppningsvis är principen i övrigt OK.
Fick det här nu. Jag utgår från det och fortsätter på projektet! Skapar nog en ny tråd om jag behöver ytterligare hjälp, tack så mycket så länge! :)






