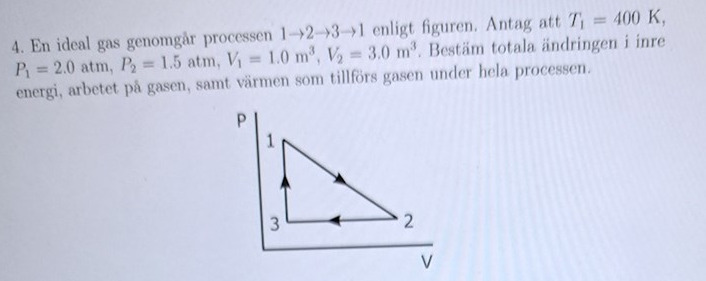
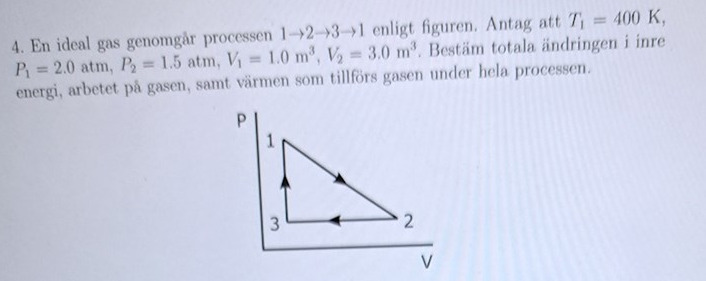
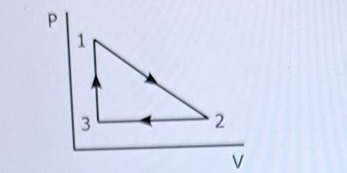
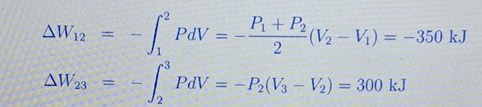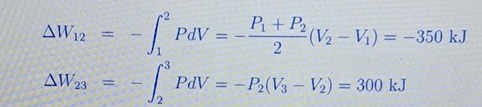Total ändringen i inre energi,arbetet på gasen samt värme som tillförs (Fysik/Universitet)

destiny99 skrev:
Hej!

Så första lagen är DU=DW+DQ. Men hur ska jag börja med denna uppgift? Om temperaturen är konstant dvs T1 under hela processen så är delta U noll?

Vad är det i uppgiften som får dig att tro att temperaten är konstnant?

Det gäller hela tiden att PV = nRT, och n och R ändras inte. Då har vi att PV/T = konstant. I fall 1 har vi P₁V₁/T₁ = 2,0^.1,0/400 = 0,005 med de angivna siffrorna och enheterna, i fall 2 blir det så P₂V₂/T₂ = 0,005 => T₂ = 200P₂V₂ = 200^.1,5^.3,0 = 900 K.

Smaragdalena skrev:
destiny99 skrev:
Hej!

Så första lagen är DU=DW+DQ. Men hur ska jag börja med denna uppgift? Om temperaturen är konstant dvs T1 under hela processen så är delta U noll?

Vad är det i uppgiften som får dig att tro att temperaten är konstnant?

Det gäller hela tiden att PV = nRT, och n och R ändras inte. Då har vi att PV/T = konstant. I fall 1 har vi P₁V₁/T₁ = 2,0^.1,0/400 = 0,005 med de angivna siffrorna och enheterna, i fall 2 blir det så P₂V₂/T₂ = 0,005 => T₂ = 200P₂V₂ = 200^.1,5^.3,0 = 900 K.

Det är just det här med inre energi som fick mig att tro det. Nu har vi två st temperaturer för att räkna ut inre energi.

Nja, det är förmodligen tre olika temperaturer, jag har inte räknat ut vad temperaturen i punkt 3 är. Vi vet ju att P₃ = P₂ = 1,5 och att V₃ = V₁ = 1 (nu hoppar jag över enheterna). Vad blir T₃?

Smaragdalena skrev:
Nja, det är förmodligen tre olika temperaturer, jag har inte räknat ut vad temperaturen i punkt 3 är. Vi vet ju att P₃ = P₂ = 1,5 och att V₃ = V₁ = 1 (nu hoppar jag över enheterna). Vad blir T₃?

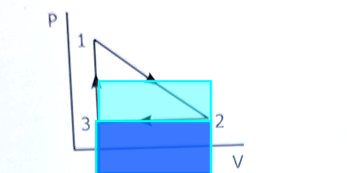
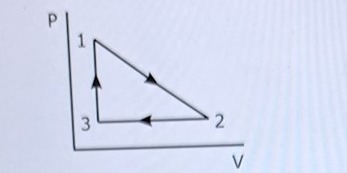
Okej. Hur vet du att P_3=P_2 och V_3=V_1? Jag hänger inte med nu. I punkten 1 är P_1=2 atm och P_2= 1.5 atm.

destiny99 skrev:

Okej. Hur vet du att P_3=P_2 och V_3=V_1? Jag hänger inte med nu.

Pieter Kuiper skrev:
destiny99 skrev:

Okej. Hur vet du att P_3=P_2 och V_3=V_1? Jag hänger inte med nu.

Summan av tryck i punkten (1) och (2) är totalt 3.5 atm. Den summan är alltså lika med tryck i punkten 3?

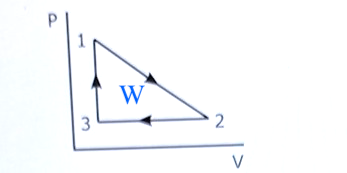
Man kan själv skriva de givna värden på diagrammets axlar.

Pieter Kuiper skrev:
Man kan själv skriva de givna värden på diagrammets axlar.

Isåfall förstår jag varför P_2=P_3 för båda punkterna har samma y koordinat.

Smaragdalena skrev:
Nja, det är förmodligen tre olika temperaturer, jag har inte räknat ut vad temperaturen i punkt 3 är. Vi vet ju att P₃ = P₂ = 1,5 och att V₃ = V₁ = 1 (nu hoppar jag över enheterna). Vad blir T₃?

Jag får det till T₃= 300K mha detta samband :

P₂*V₂/T₂=P₃*V₃/T₃. Vi vet att P₂ =P₃ och V₃=V₁=1 m³

Har du de värden som behövs för att kunna lösa uppgiften? Om inte: vad saknar du, o h hur kan du räkna ut det?

Smaragdalena skrev:
Har du de värden som behövs för att kunna lösa uppgiften? Om inte: vad saknar du, o h hur kan du räkna ut det?

Jo men det har jag. Så ändringen i inre energi är alltså delta U =3/2NkdeltaT?

Jag förstår inte varför facit tar medelvärdet av P1 och P2 när de tar skillnaden av volymerna för delta W₁₂?

destiny99 skrev:

Jag förstår inte varför facit tar medelvärdet av P1 och P2 när de tar skillnaden av volymerna för delta W₁₂?

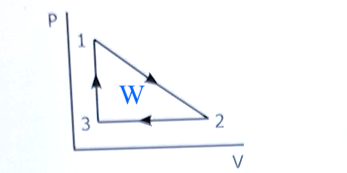
Facit räknar ut triangelns area.

Pieter Kuiper skrev:
destiny99 skrev:

Jag förstår inte varför facit tar medelvärdet av P1 och P2 när de tar skillnaden av volymerna för delta W₁₂?

Facit räknar ut triangelns area.

Varför gör de det?

destiny99 skrev:
Pieter Kuiper skrev:
Facit räknar ut triangelns area.

Varför gör de det?

Det är vad arbetet på gasen är.

Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
Facit räknar ut triangelns area.

Varför gör de det?

Det är vad arbetet på gasen är.

Okej men de gör inte det på W_23 eller W_31?

destiny99 skrev:
Pieter Kuiper skrev:
Det är vad arbetet på gasen är.

Okej men de gör inte det på W_23 eller W_31?

Det är arbetet W som är triangelns area i pV-diagrammet. Det är summan av dessa integraler. Eller man räknar ut det som halva rektangels area.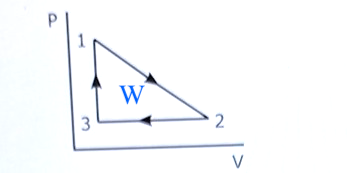

Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
Det är vad arbetet på gasen är.

Okej men de gör inte det på W_23 eller W_31?

Det är arbetet W som är triangelns area i pV-diagrammet. Det är summan av dessa integraler.

Okej men om vi integrerar från V1 till V2 för W_12 så borde det bli P1+P2(V2-V1)?

destiny99 skrev:
Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
Det är vad arbetet på gasen är.

Okej men de gör inte det på W_23 eller W_31?

Det är arbetet W som är triangelns area i pV-diagrammet. Det är summan av dessa integraler.

Okej men om vi integrerar från V1 till V2 för W_12 så borde det bli P1+P2(V2-V1)?

Eller man räknar ut det som halva rektangelns area: $W = \frac{1}{2}(P_1-P_2)(V_1-V_2) = \frac{1}{2}(2-1,\!5)\cdot 10^5 \times (3,\!0 - 1,\!0) = 50 \ {\rm kJ}$ .

Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
Det är vad arbetet på gasen är.

Okej men de gör inte det på W_23 eller W_31?

Det är arbetet W som är triangelns area i pV-diagrammet. Det är summan av dessa integraler.

Okej men om vi integrerar från V1 till V2 för W_12 så borde det bli P1+P2(V2-V1)?

Eller man räknar ut det som halva rektangelns area: $W = \frac{1}{2}(P_1-P_2)(V_1-V_2) = \frac{1}{2}(2-1,\!5)\cdot 10^5 \times (3,\!0 - 1,\!0) = 50 \ {\rm kJ}$ .

Halva rektangelns area? Var får du det ifrån?

destiny99 skrev:
Pieter Kuiper skrev:
Eller man räknar ut det som halva rektangelns area: $W = \frac{1}{2}(P_1-P_2)(V_1-V_2) = \frac{1}{2}(2-1,\!5)\cdot 10^5 \times (3,\!0 - 1,\!0) = 50 \ {\rm kJ}$ .

Halva rektangelns area? Var får du det ifrån?

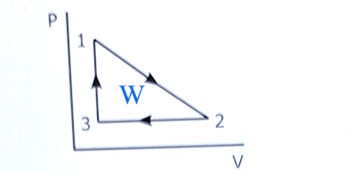
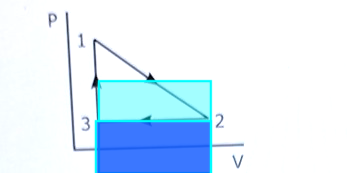
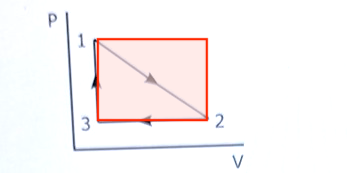Triangeln (arbetet på gasen i pV-diagrammet) har halvt så stor yta som rektangeln som jag ritade där.

destiny99 skrev:

Här är facit mindre bra.

Svaret är att ∆U = 0 alltid måste gälla i en termodynamisk cykel eftersom intern energi U är en tillståndsstorhet. Så det gäller även för vatten med ånga, för kylmedlet i luftkonditioneringen, osv osv.

Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
Eller man räknar ut det som halva rektangelns area: $W = \frac{1}{2}(P_1-P_2)(V_1-V_2) = \frac{1}{2}(2-1,\!5)\cdot 10^5 \times (3,\!0 - 1,\!0) = 50 \ {\rm kJ}$ .

Halva rektangelns area? Var får du det ifrån?

Triangeln (arbetet på gasen i pV-diagrammet) har halvt så stor yta som rektangeln som jag ritade där.

Men varför tar man skillnaden i tryck? Är det för att tryck varierar i punkten 1 och 2 medan i punkt 2 och 3 är den konstant?

destiny99 skrev:

Du verkar fråga om dessa integraler.

Arean under processen från 1 till 2 är medelvärdet av trycket multiplicerad med skillnaden i volym.

Sedan subtraherar man arean under 2 till 3.

Resultatet är lika med triangelns area.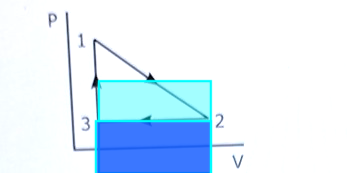

Pieter Kuiper skrev:
destiny99 skrev:

Du verkar fråga om dessa integraler.

Arean under processen från 1 till 2 är medelvärdet av trycket multiplicerad med skillnaden i volym.

Sedan subtraherar man arean under 2 till 3.

Resultatet är lika med triangelns area.

Varför är det medelvärdet av trycket för process 1 till 2?

destiny99 skrev:
Pieter Kuiper skrev:
destiny99 skrev:

Du verkar fråga om dessa integraler.

Arean under processen från 1 till 2 är medelvärdet av trycket multiplicerad med skillnaden i volym.

Sedan subtraherar man arean under 2 till 3.

Resultatet är lika med triangelns area.

Varför är det medelvärdet av trycket för process 1 till 2?

Det är trapetsmetoden för numerisk approximation av integraler: https://sv.wikipedia.org/wiki/Trapetsregeln

Den är exakt is sådana här fall.