Tolkning graf/funktion och derivata
Hej,
Skulle behöva få denna förtydligad. Jag e relativt med på att svaret är b. Iinternvallet x=2 och x= 0 så är derivatan positiv, men kan någon förklara o visa på bild varför övriga alternativ e felaktiga.
Mvh/H
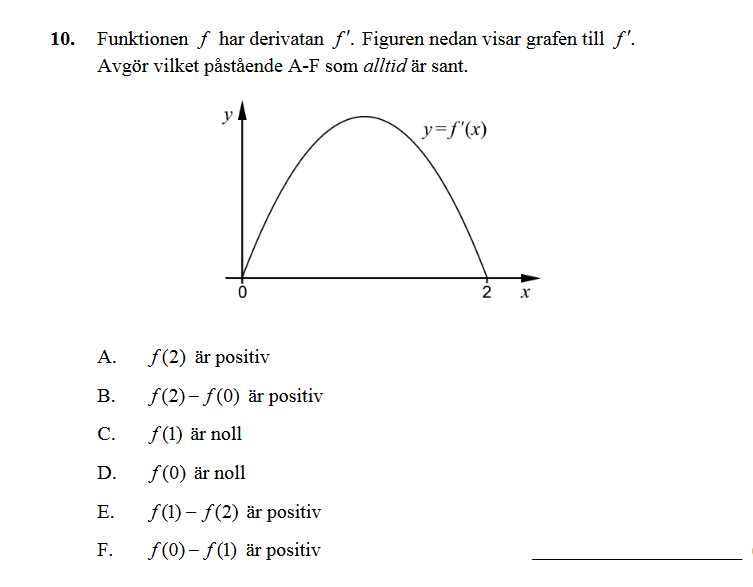
Har du ritat en funktion som skulle kunna vara f(x) ? Du vet inte exakt hur f(x) ser ut, men du vet ganska mycket om den.
Jag säger också: rita! Det är aldrig fel.
Du får en hint också, som man vanligen missar när man integrerar:
Visa spoiler
Exempel (inte din funktion):
f'(x)=2x ger f(x)=x2+C (där C förstås kan vara <0)
Hej,
Jag e osäker på hur funktionen är och ser ut, med dess egenskaper kan ni rita så ser o förstår jag?
Om derivatan är positiv mellan 0 o 2, ska funktonen f vara positiv, dvs stiga, gå uppåt där?
Mvh/H
Där derivatan är positiv är funktionen växande, men det säger inget om funktionen är större eller mindre än 0.
Hej alla o T,
Kan någon rita upp denna så jag förstår den med dess olika alternativ som e falska.
Mvh/H
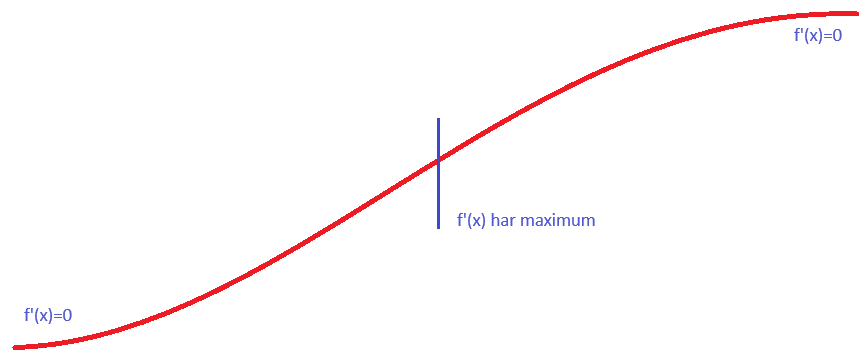
Det är inte så magiskt. f(x) kan se ut så här, ungefär. Notera att jag inte ritat ut några axlar.
Henrik 2 skrev:Hej alla o T,
Kan någon rita upp denna så jag förstår den med dess olika alternativ som e falska.
Mvh/H
Nej, men vi kan ge dig lite tips om hur du kan rita:
Vi ser att derivatan är 0 när x = 0 och när x = 2, d v s då har funktionen någon sorts extremvärde
Derivatan är positiv när 0 < x < 2, så funktionen växer i hela intervallet
OM det är så att derivatan är en andragradskurva (det ser ut så), så är funktionen en tredjegradskurva som har en extrempunkt när x = 0 och en när x = 2 och lutar så här däremellan: / så i stort sett lutar kurvan så här: \ utom just där i mitten.
Vi har ingen aning om hur stora y-värdena är för funktionen, så man kan gissa på vad som helst.
Kan du rita en kurva som stämmer med de här förutsättningarna?
Hej,
Tack för input, nej kan inte det, än, e inte med på hur man/jag gör o ser detta.
Detta förstår jag men inget mer, dvs alternativ 2 som e korrekt.
Vi ser att derivatan är 0 när x = 0 och när x = 2, d v s då har funktionen någon sorts extremvärde
Derivatan är positiv när 0 < x < 2, så funktionen växer i hela intervallet
Behöver, som jag skrev någon som ritar upp den o utifrån det förklara varför dem övriga alterativen e falska, Du säger nej, men jag säger jo..:)
Jag förstår o kan inte riktigt se hur funktionen, dvs 3dje gradaren går o vad som menas med dem andra alternativen så behöver någon som ritar upp det för mig o förklarar utifrån det.
Mvh/H
Du ser att jag skissade en graf för en stund sedan?
Hej S,
Jo, såg det,tack. Hur hjälper den mig att förstå ,kan du försöka förklara?
Vet inte om jag förstår den. E f prim (x)=0 nollställen på derivatan?
F prim (X) har maximum?
Mvh/H
Vet du vad det betyder att derivatan är noll, eller derivatan har ett maxvärde?
Hinner inte skriva så mycket nu, men tror inte det skadar att läsa på lite om derivator: Derivata (Matte 3) – Matteboken
Hej ,
Jo, det vet jag, när derivatan är noll så har den en extrempunkt,max som min eller terrasspunkt.
Men kunde dock inte tolka det du skissade ,var det en min respektive en max punkt där de är =0
Men sedan stod det med blå vertikal linje f prim (x) har ett maximum ,förstod inte den punkten. Men det e f som man kikar på och inte f prim,men hur tolkar man det?
Mvh/H
E ingen expert på derivator,dock läst på en hel del för en grundläggande förståelse, dock lite problematiskt ibland att tolka vad andra menar och med dess kurvor/linjer/grafer.
Mvh/H
f'(x) är noll för x-värdet 2. Det betyder att f(x) har lutningen noll vid x-värdet 2. f(x) är vågrät precis vid x-värdet 2.
Samma sak vid x-värdet 0.
f'(x) är större än noll för alla x-värden mellan 0 och 2. Det betyder att f(x) lutar uppåt där.
Det är allt man behöver veta för att rita en skiss som sictransit gjorde.
Henrik 2 skrev:Hej ,
Jo, det vet jag, när derivatan är noll så har den en extrempunkt,max som min eller terrasspunkt.
Men kunde dock inte tolka det du skissade ,var det en min respektive en max punkt där de är =0
Men sedan stod det med blå vertikal linje f prim (x) har ett maximum ,förstod inte den punkten. Men det e f som man kikar på och inte f prim,men hur tolkar man det?
Mvh/H
Vi kan ju ana att f(x) har ett maximum vid x=2 eftersom f’(x) nog blir negativt sedan. När f’(x) har ett maximum så är lutningen av f(x) som störst.
Så här!
Jag har plottat i grönt något som kan matcha din f'(x):
Sedan har jag tagit den primitiva funktionen av f'(x) och plottat i orange:
Därefter har jag satt C=0.
Då ser mina kurvor ut så här:
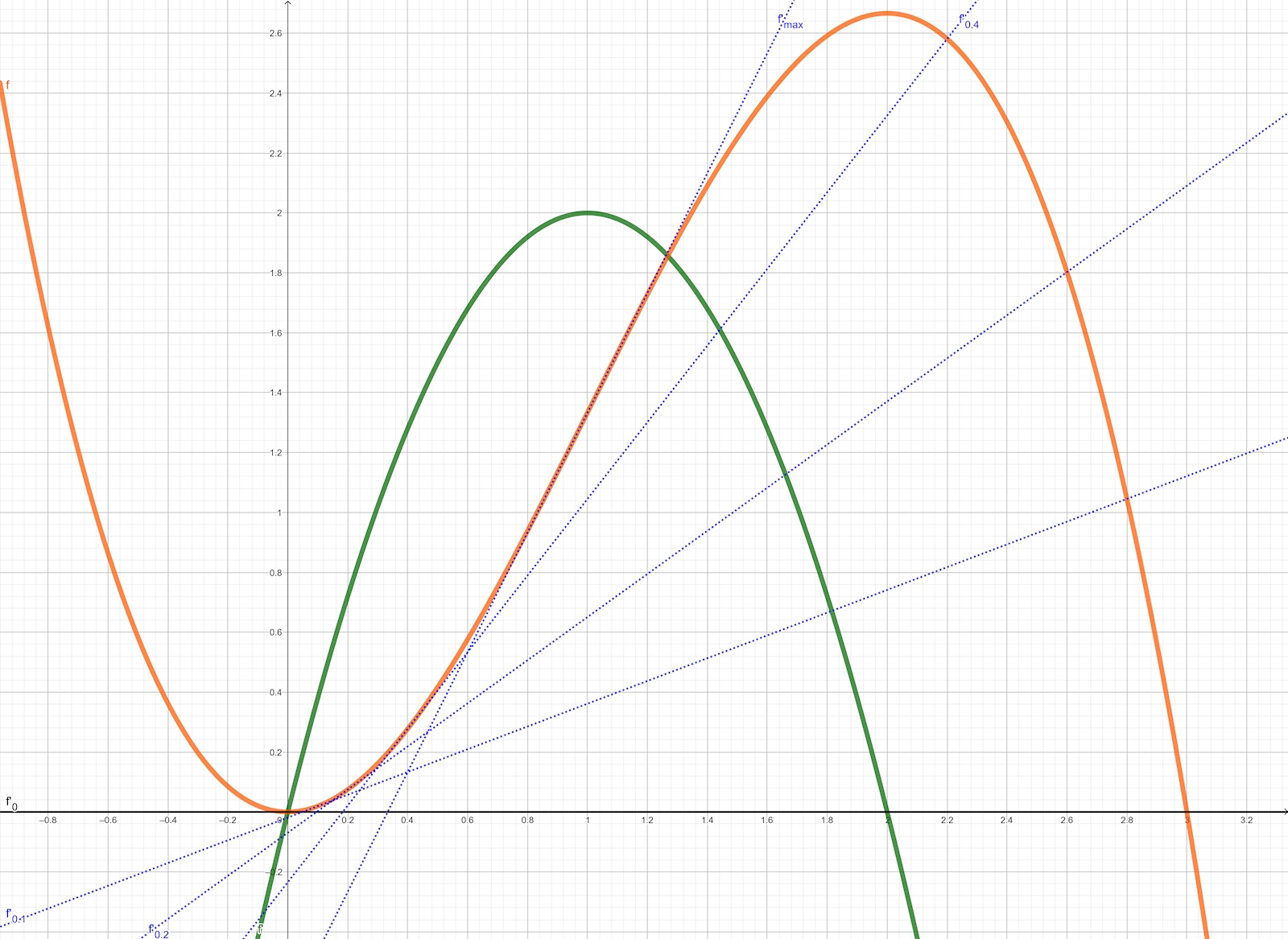
De prickade blå linjerna är tangenter till f(x), med lutningen f'(x).
Notera att vid f'(1) är lutningen som störst. Hade jag ritat ut tangenten för f'(0) eller f'(2) skulle de ha sammanfallit med x-axeln.
Viktigt att notera är det C som finns i den primitiva funktionen ovan. Nu satte jag det =0, men det kan vara hur stort, eller hur litet som helst. Min f(x) befinner sig över x-axeln för 0<x<2. Om C är negativt, kommer den inte att göra det.
Hej S,
Tackar, ser om jag ka tolka den o förstår.
Mvh/H



