Tolkning graf/er
Hej,
Har nedan ritat upp med kråkfötter sex st olika grafer i två rader. Man förstår förhoppningsvis, graferna och hur man ska tolka dem, men jag förstår inte hur man tolkar dessa o frågan.
Vilken/vilka är grafen/erna till f prim(-x)= f prim(x)?
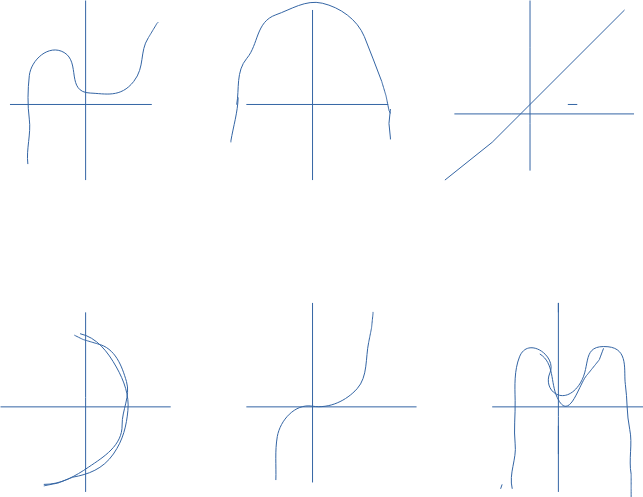
Måste vara de graferna som är symmetriska kring y-axeln.
2 & 6
Där är f(-x)=f(x), spelar ingen roll om de är f'(x)=f'(-x)
Nr 4 är en graf, men det är inte grafen för en funktion, Är det rätt ritat?
Korra skrev:Måste vara de graferna som är symmetriska kring y-axeln.
2 & 6
Där är f(-x)=f(x), spelar ingen roll om de är f'(x)=f'(-x)
Nej, om f(-x) = f(x), så är f'(-x) = -f'(x).
Så vi ska snarare leta efter f(x) = -f(-x). (eventuellt plus en konstant)
Henrik 2 skrev:[...],
Har nedan ritat upp med kråkfötter sex st olika grafer i två rader.
Det har redan skapats förvirring kring vad frågan är och vad graferna representerar.
För att undvika detta uppmanar jag dig att ladda upp en bild på uppgiften
Hej,
Tack för input, som sagt detta är vad jag har varken mer eller mindre,och jag ber då om ursäkt om det e förvirrande det jag ritar upp med kråkfötter o skriver. Men då får man om så hjälpa till med input utifrån det som jag har o visar här, dvs har inga bilder.
Mvh/H
P.s tycker att det lät rimligt det som Korra sade i inlägg 2, stämmer inte det?
Tack
Har du facit ?
Hej,
Nej, har inte det,därför jag frågar, för jag förstår inte hur man ska tolka denna. Och även om folk tycker att någon graf inte är grafen för en funktion o det andra med det tredje så var det ungefär så här fråga löd o graferna såg ut, på ett ungefär. Så borde i vart fall,tycker jag,kunna spekulera o inte bara anklaga mig,som folk gör ibland lite väl ogrundat tycker jag, e olustigt för mig när jag försöker, o har inte mer info,även om det jag gör o lägger in e lite förvirrande kan dem behålla det för sig själva ,jag försöker ju, så lite orättvist o hårda ord, men men. Tror du att ditt tänk e rätt? Förstod ingenting av frågan,men ditt resonemang lät bra för mig i vart fall, men vad vet jag, då du sade detta om att dem e symmetriska på - o + sidan..:)
Men som Laguna eller om det var Trinity sade var det kanske fel..Förstod dock ingenting av inlägg 4.
Mvh/H
Bump, även om ni tycker detta e otydligt med mina grafer. Det e det som jag har o kommer ihåg. Behöver förstå o spekulera i denna . Jag förstår den inte alls, men Korras input ,graf 2 o 6, i o m att dem e symmetriska kring y-axeln.
Rita de här i Desmos: x3-4x+4, 4-x2, x, x3 och 4x2-x4.
Tackar, har dock inte ritat i det programmet så vet inte hur man gör. Är det fem st olika ekvationer eller vad man kallar det som du nu skrev att jag skulle rita in?
Är inne på Desmos nu o står i rutan man skriver in i. Så vart hittar jag de olika tecknen,t ex. upphöjt till,navigera mig e du,ni snälla.
Mvh/H
För att skriva in x2 skriver du x^2. Tecknet ^ sitter på tangenten till höger om å, och du behöver använda shift för att få fram det.
Ok, så det finns inga sådan här tecken i själva Desmos?
Då testar jag med denna tanget på tangetbordet.
Nix, funkar inte när jag står i rutan att göra på det sättet. När jag skriver in det någon annanstans med shift o själva tecknet funkar det men står jag i rutan i Desmos så funkar det inte...såklart..)
Finns det tecken i Desmos som man kan använda sig av?
Som jag svarade i din andra tråd: Klicka på tangentbordssymbolen i nedre vänstra hörnet och undersök vad som finns där.
Såg inte den än, men vad bra nu så. Då skriver jag in dem o ser vad jag får ut. Vad ska jag se o tolka av dessa grafer?
Lägg upp graferna här så kan vi hjälpa dig att tolka dem.
Meningen var att de skulle likna de grafer som du visade i din bild.
Tolka vet jag inte.
För att skriva x2 i Desmos trycker du först på x, sedan på a2.
Om du vill ändra exponenten till något annat så kan du redigera den

 Så vad ska göras med denna som liknar mina grafer?
Så vad ska göras med denna som liknar mina grafer?
Ops, kom in dubbelt
Behöver ju hjäp med
Vilken/vilka är grafen/erna till f prim(-x)= f prim(x)?
Mvh/H
Henrik 2 skrev:
Så vad ska göras med denna som liknar mina grafer?
Ops, kom in dubbelt
Behöver ju hjäp med
Vilken/vilka är grafen/erna till f prim(-x)= f prim(x)?
Mvh/H
Bra Henrik!
Det är ett stort steg framåt att du har börjat använda Desmos, tagit screenshot och klistrat in bild här.
Nu tror jag att det kommer att bli mycket enklare att hjälpa dig framöver när även du kan använda grafer för att beskriva vad du menar.
Du kan redigera ditt inlägg och ta bort den ena bilden - sådant gör jag ofta, när jag ser att mitt inlägg inte blev riktigt som jag hade tänkt.
Den blå linjen är rät, d v s den har formeln y = kx+m.
Den gröna ser ut att vara en andragradare med negativ koefficient för kvadrattermen.
Den svarta ser ut att vara x3.
Den ena röda ser ut mycket förenklat så här: / då är den högsta potensen udda. Den andra röda ser väldigt förenklat ut så här U fast upppochner - då är den högsta potensen jämn och koefficienten för denna term är negativ.
Vet, men för sent nu, o försökte men när jag tog bort ena så försvann den andra..:)
Men hur löser o tolkar mandå graferna?
Förstår inte hor man tolkar frågan o då graferna o vilken elelr vilka det är?
Vilken/vilka är grafen/erna till f prim(-x)= f prim(x)?
Hej,
Jag kan ge mig på ett försök till en lösning, då jag tycker frågan är ologisk. Jag gissar att det stod mer i uppgiften, kanske var det inte generellt f'(-x)=f'(x) utan att det kanske skulle finns några specifika punkter på kurvan där detta skulle vara sant.
Om så är fallet, finns det flera punkter där detta stämmer.
Betrakta denna funktion:
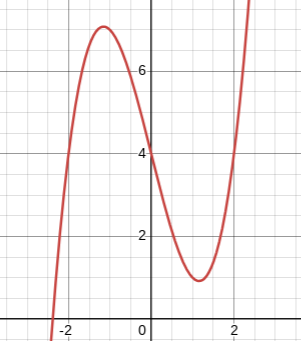
Finns det två punkter på kurvan där villkoret uppfylls?
Hej,
Nja, frågan löd att man skulle välja ut en eller två av de grafer som jag försökte mig på att rita med kråkfötter. Jag förstår den inte o kan inte heller tolka detta. Hur tolkar man generellt f prim (-x) =f prim (x)?
Mvh/H
Att f'(-x) = f'(x) innebär att grafen till y = f'(x) är symmetrisk med avseende på y-axeln.
Dvs om du har grafen på ett papper och viker detta papper längs med y-axeln så kommer grafen på ena halvan av papperet att exakt överlappa grafen på den andra halvan av papperet.
Ett exempel på ett sådant samband är f'(x) = x2.
Det uppfyller sambandet f'(-x) = f'(x) eftersom f'(-x) = (-x)2 = x2 = f'(x)
Hittar du samma egenskaper hos någon av de 6 givna graferna?
====
Jag förutsätter här att graferna visar sambanden y = f'(x) och att frågan gäller vilken/vilka av dessa grafer som passar in på sambandet f'(-x) = f'(x).
Hej Y,
Bra att du svarade också. Så var graf 2 o 6 korrekt då dem e symmetriska precis som Korra sade i ett av de tidigare inläggen.
Mvh/H
Ja, enligt hur geafeena troligtvis såg ut och hur uppgiften troligen var formulerad så är svaret graf 2 och 6.
De flesta verkar mena att det är f' vi ser i graferna. Jag tycker det är troligare att det är f.
Jag tolkar likt Laguna att det är funktionen f(x) som grafen visar och att man utifrån den ska utläsa var villkoret gäller. I mitt exempel gäller det där derviatan = 0.
Laguna skrev:De flesta verkar mena att det är f' vi ser i graferna. Jag tycker det är troligare att det är f.
Jag håller med dig om det, men det beror på vilken nivå av kunskap frågan vill testa
Vi vet inte hur frågan lyder i original och vi vet inte om det är en "A"- fråga eller inte.
Vi kan ju göra andra tolkningar också.
T.ex. att graferna visar sambanden y = f(x) och frågan gäller vilka av dessa stämmer med f'(-x) = f'(x)
Eller att graferna visar sambanden y = f'(x) och frågan gäller vilka av dessa stämmer med f(-x) = f(x)
Hm, debatterande om uppgiften , vad bra. Frågan ligger tror jag på A till C nivå.
Mvh/H
Så kan man, även om man inte riktigt vet då frågan e otydlig såsom mina grafer, tolka det som att det handlar om symmetrin vid y-axeln o således graferna 2 o 6?
Mvh/H
Henrik 2 skrev:Så kan man, även om man inte riktigt vet då frågan e otydlig såsom mina grafer, tolka det som att det handlar om symmetrin vid y-axeln o således graferna 2 o 6?
Mvh/H
Nej, man kan inte tolka en fråga som är så otydligt skriven som din, däremot kan man gissa.
Henrik 2 skrev:Så kan man, även om man inte riktigt vet då frågan e otydlig såsom mina grafer, tolka det som att det handlar om symmetrin vid y-axeln o således graferna 2 o 6?
I slutet av svar #25 skrev jag följande:
Jag förutsätter här att graferna visar sambanden y = f'(x) och att frågan gäller vilken/vilka av dessa grafer som passar in på sambandet f'(-x) = f'(x).
Om vi säger att denna tolkning gäller så är rätt svar "Graf 2 och 6".
Mmm, ja jag får nöja mig med det svaret då jag, som oftast, inte har helt tydliga o utformade frågor.
Enligt en tolkning är det graferna 2 och 6 och nu stannar vi vid det o spekulerar inte mer,för det e ingen annan som har kommit något förslag om övriga grafer.
Nej, det var så frågan löd ,inte speficika punkter på kurvan där det skulle vara sant, utan e säker på att det var i vart fall f'(-x)=f'(x).
Så nu e denna uppgift diskuterad o "färdig"
Mvh/H





