Tolkning att derivatan till en konstant funktion är noll
Förklara, med hjälp av derivatans definition, varför derivatan till en konstant funktion är noll
Derivatan av den konstanta funktionen f ( x ) = c är lika med noll eftersom den inte förändras då variabeln ändras. Detta kan visas med derivatans definition:
f prim (x)= lim h>0 f (x+h) - f (x)/ h = lim h>0 c-c/h= lim h>0 0/h= 0
Kan någon förklara denna konkret med tal/siffor. Förstår men ändå inte till 100..
Konstant funktion f (x)=c? c-c/h?
Pratar vi om vilket tal som helst som e en konstant och som försvinner när man deriverar?
Mvh/H
Hej,
Jag antar att det du skrivit är facit.
Konstanten c är vilket tal som helst, alltså kan vara 5, 2222, -3, osv.
Ser du att c-c = 0?
Det lämnar kvar 0 i täljaren, om man delar med 0 med vad som helst förblir det 0, därför är derivatan av en konstant helt enkelt 0.
Prova att sätta in talet 25 istället för x och utför derivatans definition, alltså med funktionen f(x)=25.
Vad får du för derivata?
Hej,
Jo, ok, man får c-c, t ex 25-25=0 som blir 0 när man delar det med nämnaren och således är derivatan av en konstant alltid 0.
Vet inte riktigt men f prim (Ska man ha funktionen eller derivatan här efter f?)(25+h)- f (25)/h= 25+h-25/h= 0+h/h=0
När man sätter in 25 istället för x ska man inte ha h i täljaren kvar?
Mvh/Henning
Jo. h hänger alltid med.
Hej M,
Ok, men då det e c-c=0 som blir kvar är det så att h som följer med går mot 0 ,d v s lim h>0 och således så hänger den med men går ju mot 0 så den räknas lisom inte med när man skriver c-c?
Mvh/H
Jag tror att jag missförstod din förra fråga.
Här är hur gränsvärdet kan uttryckas för en konstant:
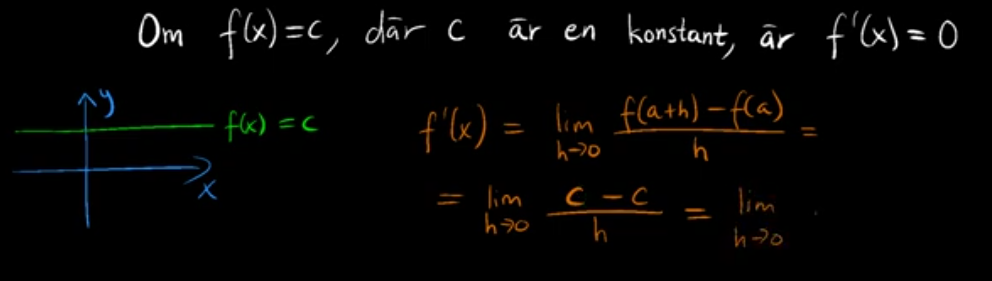
Detta är från en video av Mattecentrum: https://youtu.be/bg5O0ROOiik
Eftersom funktionen inte beror på någon variabel kommer h inte att finnas med i täljaren. När man subtraherar konstanten med samma värde, blir det 0 i täljaren, och derivatan blir således också 0.
Hej,
Så h finns inte med i ekvationen/funktionen, vet inte om jag hänger med riktigt. H:et finns ju där vad görs med den förstår inte riktigt det?
Men den finns helt enkelt inte med utan bara konstanter räknas med,ok.
Mvh/H
När man skriver f(x+c) ska man alltså "anropa" funktionen f med argument x+c.
Vi ersätter alltså x med inputen x+c
- Om f(x)=3x kommer f(x+h)=3(x+h), eftersom vi ersätter x med x+c
- Om f(x)=3 kommer f(x+h)=3, vi ersätter x med x+c, men eftersom det inte finns något x kan vi inte sätta in något x+c.
Hej,
Vet inte om jag blev myckt klokare av den förklaringen, förstod inte.
Hnadlar det om att när vi dervierar försvinner konstanten?
Jag förstår inte, så om du tar ett exempel med variabler och konstanster så jag kan se o härleda din förklaring.
Mvh/H
Handlar
Deriverar
Konstanter
I den ena förklaringen så ska jag sätta in o ersätta x:et med t ex 25,ok. Och sedan så undrar jag om h, vad som händer med den, och då får jag til svar att x försvinner. Ja om man har 3x så försvinner x:et i deriveringen men förstår inte vad man vill ha ut av denna förklaring/definition. Ska man kika på x eller h, x:et e väl variabeln och h e konstanten ?
Mvh/H
Du har blandat till det verkar det som.
Läs här och återkom med tydliga frågor i formatet: 1.XYZ?
https://www.matteboken.se/lektioner/matte-3/derivata/derivatans-definition#!/
https://www.matteboken.se/lektioner/matte-3/derivata/deriveringsregler#!/
Hej M,
Blandat, jo såklart,men när man inte e sådant mattesnlle o får olika förkalringar från er, som jag tycker, när man inte behärskar definition o vad som händer o sker blir det så. Kikar länk.
Men ett exempel skulle vara bra för förståelsen.
Mvh/H
Ok, refererar till det som Calle skrev. Så om vi har f (x)= 25x så f(x+h)= 25(x+h) men om bara x:et ersätts med 25 således finns inte x som man kan sätta in x+c ?
Mvh/H
Om vi har funktionen f(x) = 25x så har vi inte en funktion som är konstant. Om vi har en funktion som är f(x) = 25 har vi en funktion som är konstant, d v s en funktion som ger samma utvärde vilket värde vi än stoppar in.
Ok..::)



