Tjena! Undrar om denna uppgiften går att lösa

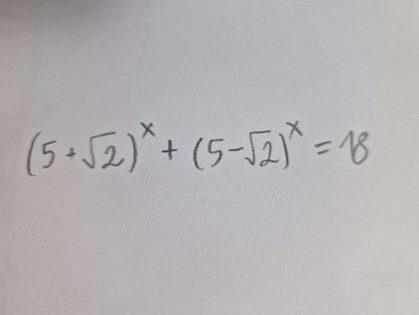
Har väldigt svårt att se att det skulle finnas en analytisk lösning till denna. Jag skulle löst den numerisk, t.ex. med metoden nedan.

Så att gissa sig fram till uppgiften är det ett bra sätt att lösa uppgiften?

Coolcat35 skrev:

Så att gissa sig fram till uppgiften är det ett bra sätt att lösa uppgiften?

Vänsterled för x=1 är 10 och för x=2 är 54 = 3 × 18.

Är du säker att du skrev rätt uppgift? Räkna $(2+\sqrt{5})^2 + (2-\sqrt{5})^2$... slump??

Coolcat35 skrev:

[....]

Miniräknare sa läraren att man skulle avstå från att använda!

Välkommen till Pluggakuten!

Då sa nog läraren fel. Digitala hjälpmedel är ett måste för denna ekvation.

Sådana här uttryck får man när man löser differensekvationer, alltså t.ex. a_n+2 = a_n+2a_n-1.

Om man tar reda på vilken differensekvation uttrycket är lösning till så blir det lösbart, förutsatt att x är ett heltal.

Som Pieter Kuiper var inne på i #4, så vill jag nog tro att uppgiften är fel avskriven.

Hade det varit  $(\sqrt{5} + 2)^x + (\sqrt{5} - 2)^x = 18$,  så vore ekvationen faktiskt lösbar algebraiskt, utan miniräknare/dator.

Notera att konjugatförlängning ger att

$\sqrt{5} - 2 = \left(\sqrt{5} - 2\right) \cdot \dfrac{\sqrt{5} + 2}{\sqrt{5} + 2} = \dfrac{5-4}{\sqrt{5} + 2} = \dfrac{1}{\sqrt{5} + 2}$.

Gör man ett variabelbyte $t = (\sqrt{5} + 2)^x$, så blir ekvationen  $t + \dfrac{1}{t} = 18$ vars lösningar är $t_{1,2} = 9 \pm 4\,\sqrt{5}$.

Notera nu att $(\sqrt{5} + 2)^2 = 9+4\,\sqrt{5}$  och  $(\sqrt{5} - 2)^2 = 9-4\,\sqrt{5}$.

Därmed går det att lösa ut $x$ ur återsubstitutionssambandet  $(\sqrt{5} + 2)^x = 9 \pm 4\,\sqrt{5}$

Ett betydligare snyggare problem av LuMa07

LuMa07 skrev:

Som Pieter Kuiper var inne på i #4, så vill jag nog tro att uppgiften är fel avskriven.

Hade det varit  $(\sqrt{5} + 2)^x + (\sqrt{5} - 2)^x = 18$,  så vore ekvationen faktiskt lösbar algebraiskt, utan miniräknare/dator.

Notera att konjugatförlängning ger att

$\sqrt{5} - 2 = \left(\sqrt{5} - 2\right) \cdot \dfrac{\sqrt{5} + 2}{\sqrt{5} + 2} = \dfrac{5-4}{\sqrt{5} + 2} = \dfrac{1}{\sqrt{5} + 2}$.

Gör man ett variabelbyte $t = (\sqrt{5} + 2)^x$, så blir ekvationen  $t + \dfrac{1}{t} = 18$ vars lösningar är $t_{1,2} = 9 \pm 4\,\sqrt{5}$.

Notera nu att $(\sqrt{5} + 2)^2 = 9+4\,\sqrt{5}$  och  $(\sqrt{5} - 2)^2 = 9-4\,\sqrt{5}$.

Därmed går det att lösa ut $x$ ur återsubstitutionssambandet  $(\sqrt{5} + 2)^x = 9 \pm 4\,\sqrt{5}$

Tack! Detta hjälpte mycket. Vår lärare försökte testa våra kunskaper så han skrev så med mening för att se om vid förstod.