Tillämpning av kedjeregeln i en kon
Hej!
Jag har fastnat i förståelsen för tillämplig av kedjeregeln när de gäller koner. Jag förstår varför man byter ut radien mot en "ekvation" för att bara få en variabel, det jag inte förstår är hur det blir just radien/ höjden (se bild nedan) då jag inte ser den koppling till detta i formeln för volymen för konen. Jag förstår det så att från lösningsförslaget min lärare givit att det är för att få förhållandet mellan hela konen och den delen som är "fylld" eftersom det är likformigt men jag har en känsla av det kan vara en feltolkning?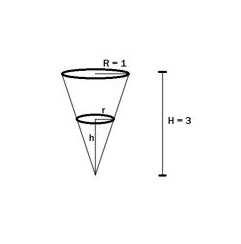

Kolla på bilden. Det är två stycken likformiga rätvinkliga trianglar. Samma förhållande mellan kateterna gäller.
Då tolkade jag alltså lösningsförlaget på rätt sätt. För jag blev förvirrad när jag läste en förklaring i matteboken där de i istället delade h med 2 där förklaringen va att diametern är lika med höjden, delas det då med två för att en kon är triangelformad? (Bas * höjd / 2)
Nej. Om höjden är lika med diametern och radien är halva diametern, så måste ju också radien vara halva höjden.
r=d/2 om d=h så gäller r=h/2
Nu är jag med! Tack för hjälpen!


