Termodynamik - Bestämma enhet, dimensioner & dimensionsanalys

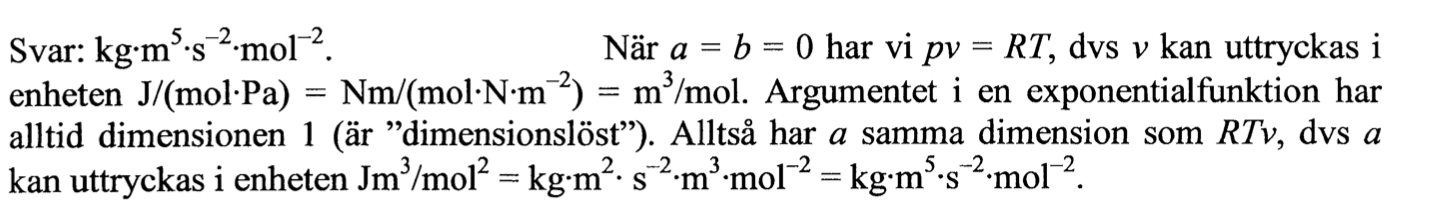
Varför sätter man a=b=0?
Luffy skrev:
Varför sätter man a=b=0?
För att bestämma att v i formeln betecknar den molära volymen.
Pieter Kuiper skrev:Luffy skrev:
Varför sätter man a=b=0?För att bestämma att v i formeln betecknar den molära volymen.
Jag hänger inte riktigt med, vad innebär molär volym och varför är det relevant för att bestämma enheten på a?
Luffy skrev:vad innebär molär volym och varför är det relevant för att bestämma enheten på a?
Molär volym är volymen per mol; vid standard temperatur och tryck är det 24 liter för en ideal gas.
Man ser att har i SI-systemet samma enhet som , alltså joule per mol. Det är kanske lite rundgång där men det är också egentligen något som kan utgå ifrån, eftersom är mekaniskt arbete per mol gas.
Det centrala i resonemanget i facit är att argument av exponentialfunktionen (och av mycket annat som t ex sinus och logaritmer) måste vara dimensionslösa för att dessa funktioner annars skulle få ett annat värde när man börjar använda ett annat enhetssystem.
Så konstanten a i formeln måste ha samma enhet som .
För en ideal gas gäller dela att den totala volymen av alla partiklar är 0, dels att krafterna mellan partiklarna är 0. När detta gäller har man den vanliga idealgaslagen, PV = nRT.
Om man inte kan försumma partiklarnas totala volym, kan man kompensera för detta genom att "krångla till" funktionen, här har man gjort detta genom att införa konstanten b. Eftersom man kna utföra subtraktionen v-b måste konstanten b ha samma enhet som volymen v, d v s b har enheten m3.
Om man inte kan försumma krafterna mellan partiklarna, kan man kompensera för detta genom att "krångla till" funktionen, i det här fallet genom att multiplicera HL med en exponentialfunktion som beror på en konstant a. Resten av resonemanget upprepar jag inte en gång till.



