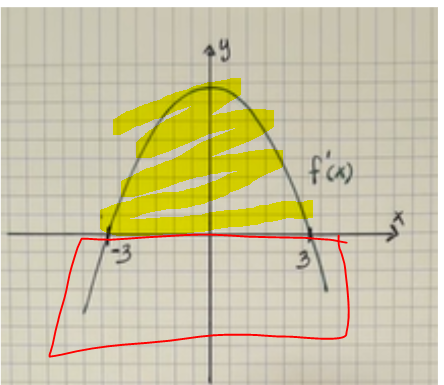
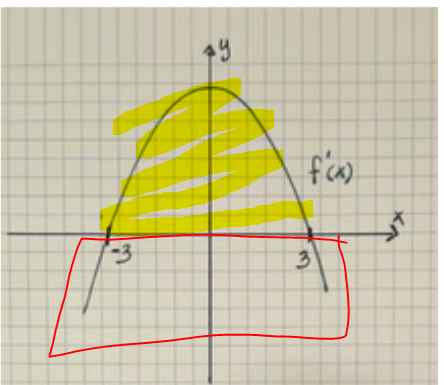
teckenväxling
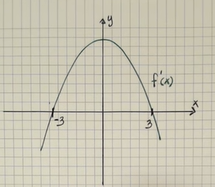
hur avgör man teckenväxlingen här för f' vid x=3?
vid punkt -3 skulle jag säga att det går från + till + men enligt facit är det från - till +
((alltså är de ute efter derivatan eller y-värdena?))
Om x = -3,1 har f'(x) värdet -0,5 ungefär, definitivt negativt, i alla fall.
Om x = -2,9 har f'(x) värdet 0,5 ungefär, definitivt positivt, i alla fall.
Alltså är teckenväxlingen vid -3 -0+. Det verkar som om du tittar på derivatans lutning, d v s andraderivatan.
Smaragdalena skrev:Om x = -3,1 har f'(x) värdet -0,5 ungefär, definitivt negativt, i alla fall.
Om x = -2,9 har f'(x) värdet 0,5 ungefär, definitivt positivt, i alla fall.
Alltså är teckenväxlingen vid -3 -0+. Det verkar som om du tittar på derivatans lutning, d v s andraderivatan.
hur avgör man det? har inte gått igenom andraderivatan än och det här kapitlet har heller inte behandlat det "området" än. så man förväntas väl kunna göra det på ett annat sätt?
Man avgör om värdet är positivt eller negativt genom det avläsa i grafen. Hur kom du fram till att det går från + till + vid x = -3, när kurvan ligger under x-axeln när x är mindre än -3?
naturnatur1 skrev:((alltså är de ute efter derivatan eller y-värdena?))
Bilden visar grafen till derivatafunktionen, dvs y = f'(x), inte y = f(x).
Om de frågar efter värdet på f'(x) så är det alltså y-värdet ur bilden de är ute efter.

Smaragdalena skrev:Man avgör om värdet är positivt eller negativt genom det avläsa i grafen. Hur kom du fram till att det går från + till + vid x = -3, när kurvan ligger under x-axeln när x är mindre än -3?
jag tyckte det såg ut som lutningen gick från + till + (alltså jag kollade bara på att linjen gick upp)
hur fick du att x = -3,1 har värdet f'(x) -0,5 och
att x = -2,9 har f'(x) värdet 0,5
drog du tangent?
ursäkta för frågorna men är nog att vi inte pratat om det i skolan
Yngve skrev:naturnatur1 skrev:((alltså är de ute efter derivatan eller y-värdena?))
Bilden visar grafen till derivatafunktionen, dvs y = f'(x), inte y = f(x).
Om de frågar efter värdet på f'(x) så är det alltså y-värdet ur bilden de är ute efter.
så om jag får en sådan graf där y = f'(x) och ska avgöra teckenväxlingen är det y värdet man kollar på?
om jag får fråga.. varför gör man det?
Är du med på att f'(x) betecknar derivatan av funktionen f(x)?
- Om nej: Läs detta avsnitt och fråga oss om allt du vill att vi förklarar närmare.
- Om ja: Är du med på att om t.ex. f'(2) = 4 så är derivatan av f(x) i punkten x = 2 lika med 4, vilket innebär att grafen till y = f(x) har lutningen 4 vid x = 2?
Yngve skrev:Är du med på att f'(x) betecknar derivatan av funktionen f(x)?
- Om nej: Läs detta avsnitt och fråga oss om allt du vill att vi förklarar närmare.
- Om ja: Är du med på att om t.ex. f'(2) = 4 så är derivatan av f(x) i punkten x = 2 lika med 4, vilket innebär att grafen till y = f(x) har lutningen 4 vid x = 2?
ja det är jag med på, men då snackar vi väl om x-värden och inte y?
naturnatur1 skrev:
ja det är jag med på, men då snackar vi väl om x-värden och inte y?
Nej, derivatan är också en funktion av x.
Egentligen borde vi säga att f'(x) är derivatafunktionen till f(x), men vi slarvar lite och säger att f'(x) är derivatan av f(x).
Det betyder att om vi har en graf som visar derivatafunktionens värden, dvs y = f'(x), så är derivatafunktionens värde vid t.ex. x = 2 lika med f'(2), vilket är lika med höjden på grafen till y = f'(x) där x = 2.
Yngve skrev:naturnatur1 skrev:ja det är jag med på, men då snackar vi väl om x-värden och inte y?
Nej, derivatan är också en funktion av x.
Egentligen borde vi säga att f'(x) är derivatafunktionen till f(x), men vi slarvar lite och säger att f'(x) är derivatan av f(x).
Det betyder att om vi har en graf som visar derivatafunktionens värden, dvs y = f'(x), så är derivatafunktionens värde vid t.ex. x = 2 lika med f'(2), vilket är lika med höjden på grafen till y = f'(x) där x = 2.
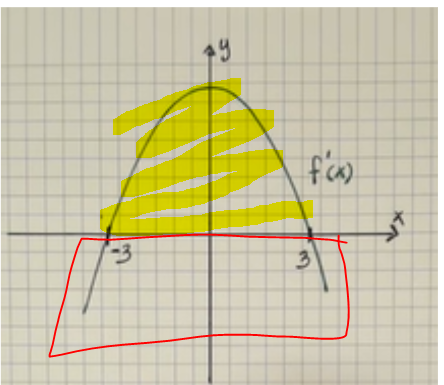
jaha, så egentligen kan man säga att eftersom det är en f'(x) graf så kan man dra slutsatsen att över x-ledet så är det +, under x-led är det - och på x-ledet är derivatan 0.
derivatan vid x = -3 är 0
men med teckenväxlingen menar de alltså +/- 0 +/- , eller? (alltså att man kollar tecknen ( +/-) innan derivatan blev 0?
naturnatur1 skrev:
jaha, så egentligen kan man säga att eftersom det är en f'(x) graf så kan man dra slutsatsen att över x-ledet så är det +, under x-led är det - och på x-ledet är derivatan 0.
Ja, eftersom grafen visar derivatafunktionen, dvs y = f'(x),så gäller det att att
- under x-axeln är f'(x) < 0
- ovanför x-axeln är f'(x) > 0
- på x-axeln är f'(x) = 0
Läs nu svaren du fått tidigare i denna tråd igen så kanske det blir tydligare.
derivatan vid x = -3 är 0
men med teckenväxlingen menar de alltså +/- 0 +/- , eller? (alltså att man kollar tecknen ( +/-) innan derivatan blev 0?
Jag vet inte vilken teckenväxling de menar utan att se själva frågan. Kan du ladda upp en bild på den?
Yngve skrev:naturnatur1 skrev:
jaha, så egentligen kan man säga att eftersom det är en f'(x) graf så kan man dra slutsatsen att över x-ledet så är det +, under x-led är det - och på x-ledet är derivatan 0.
Ja, eftersom grafen visar derivatafunktionen, dvs y = f'(x),så gäller det att att
- under x-axeln är f'(x) < 0
- ovanför x-axeln är f'(x) > 0
- på x-axeln är f'(x) = 0
Läs nu svaren du fått tidigare i denna tråd igen så kanske det blir tydligare.
derivatan vid x = -3 är 0
men med teckenväxlingen menar de alltså +/- 0 +/- , eller? (alltså att man kollar tecknen ( +/-) innan derivatan blev 0?Jag vet inte vilken teckenväxling de menar utan att se själva frågan. Kan du ladda upp en bild på den?

naturnatur1 skrev:
OK då är svaret på a-uppgiften -0+ och svaret på b-uppgiften +0-.
Är du med på det?
Yngve skrev:
OK då är svaret på a-uppgiften -0+ och svaret på b-uppgiften +0-.
ja det stämmer, kan jag då alltså ta med mig från denna uppgiften att
frågar man efter teckenväxlingen vid en viss punkt och derivatafunktionen är f' så är det y-värdet jag avläser om det är neg/pos och därmed får jag teckenväxlingen?
jag tror jag är med på det, man har att y är alltså derivatan typ?
naturnatur1 skrev:Yngve skrev:OK då är svaret på a-uppgiften -0+ och svaret på b-uppgiften +0-.ja det stämmer, kan jag då alltså ta med mig från denna uppgiften att
frågar man efter teckenväxlingen vid en viss punkt och derivatafunktionen är f' så är det y-värdet jag avläser om det är neg/pos och därmed får jag teckenväxlingen?
Ja, om grafen visar y = f'(x). Inte om grafen visar y = f(x).
jag tror jag är med på det, man har att y är alltså derivatan typ?
Se ovan.
=============
Bra att du vill förstå ordentligt. Vi tar ett par exempel så kan du känna dig säkrare.
Jag visar nu en påhittad graf y = f'(x), dvs en graf av derivatafunktionen till f(x).

Frågor:
- Har f'(x) en teckenväxling vid x = -4? I så fall vilken?
- Har f'(x) en teckenväxling vid x = -2? I så fall vilken?
- Har f'(x) en teckenväxling vid x = 0? I så fall vilken?
- I vilket/vilka intervall har funktionen f(x) en positiv lutning?
- I vilket/vilka intervall har funktionen f(x) en negativ lutning?
- I vilken/vilka punkter har funktionen f(x) en horisontell lutning?
===================
Nu visar jag en påhittad graf y = f(x), dvs en graf av funktionen f

Frågor:
- Var har f'(x) teckenväxlingar och hur ser de ut?
- I vilket/vilka intervall har funktionen f(x) en positiv lutning?
- I vilket/vilka intervall har funktionen f(x) en negativ lutning?
- I vilken/vilka punkter har funktionen f(x) en horisontell lutning?
Yngve skrev:naturnatur1 skrev:Yngve skrev:OK då är svaret på a-uppgiften -0+ och svaret på b-uppgiften +0-.ja det stämmer, kan jag då alltså ta med mig från denna uppgiften att
frågar man efter teckenväxlingen vid en viss punkt och derivatafunktionen är f' så är det y-värdet jag avläser om det är neg/pos och därmed får jag teckenväxlingen?
Ja, om grafen visar y = f'(x). Inte om grafen visar y = f(x).
jag tror jag är med på det, man har att y är alltså derivatan typ?
Se ovan.
=============
Bra att du vill förstå ordentligt. Vi tar ett par exempel så kan du känna dig säkrare.
Jag visar nu en påhittad graf y = f'(x), dvs en graf av derivatafunktionen till f(x).
Frågor:
- Har f'(x) en teckenväxling vid x = -4? I så fall vilken?
Ja, + 0 -
- Har f'(x) en teckenväxling vid x = -2? I så fall vilken?
Nej
- Har f'(x) en teckenväxling vid x = 0? I så fall vilken?
Ja, - 0 +
- I vilket/vilka intervall har funktionen f(x) en positiv lutning?
x < -4 och x > 0
- I vilket/vilka intervall har funktionen f(x) en negativ lutning?
-4 < x < 0
- I vilken/vilka punkter har funktionen f(x) en horisontell lutning?
x = -4 och x = 0
===================
Nu visar jag en påhittad graf y = f(x), dvs en graf av funktionen f
Frågor:
- Var har f'(x) teckenväxlingar och hur ser de ut?
Där x = 0 så är det - 0 +
Där x = 4 så är det + 0 -
- I vilket/vilka intervall har funktionen f(x) en positiv lutning?
0 < x < 4
- I vilket/vilka intervall har funktionen f(x) en negativ lutning?
X mindre än 0 och vid x större än 4
- I vilken/vilka punkter har funktionen f(x) en horisontell lutning?
x = 0 och x = 4
Det stämmer! Det känns som om du har bra koll på detta nu 👍
Yngve skrev:Det stämmer! Det känns som om du har bra koll på detta nu 👍
tack snälla! uppskattar verkligen din hjälp och test uppgiften jag fick!